CF1823F Random Walk

You are given a tree consisting of $ n $ vertices and $ n - 1 $ edges, and each vertex $ v $ has a counter $ c(v) $ assigned to it. Initially, there is a chip placed at vertex $ s $ and all counters, except $ c(s) $ , are set to $ 0 $ ; $ c(s) $ is set to $ 1 $ . Your goal is to place the chip at vertex $ t $ . You can achieve it by a series of moves. Suppose right now the chip is placed at the vertex $ v $ . In one move, you do the following: 1. choose one of neighbors $ to $ of vertex $ v $ uniformly at random ( $ to $ is neighbor of $ v $ if and only if there is an edge $ \{v, to\} $ in the tree); 2. move the chip to vertex $ to $ and increase $ c(to) $ by $ 1 $ ; You'll repeat the move above until you reach the vertex $ t $ . For each vertex $ v $ calculate the expected value of $ c(v) $ modulo $ 998\,244\,353 $ .

The first line contains three integers $ n $ , $ s $ and $ t $ ( $ 2 \le n \le 2 \cdot 10^5 $ ; $ 1 \le s, t \le n $ ; $ s \neq t $ ) — number of vertices in the tree and the starting and finishing vertices. Next $ n - 1 $ lines contain edges of the tree: one edge per line. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ ; $ u_i \neq v_i $ ), denoting the edge between the nodes $ u_i $ and $ v_i $ . It's guaranteed that the given edges form a tree.

Print $ n $ numbers: expected values of $ c(v) $ modulo $ 998\,244\,353 $ for each $ v $ from $ 1 $ to $ n $ . Formally, let $ M = 998\,244\,353 $ . It can be shown that the answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

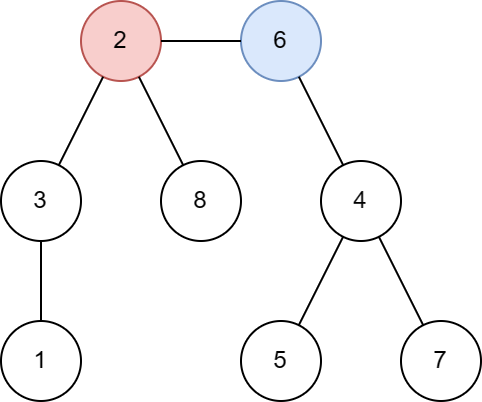
The tree from the first example is shown below:  Let's calculate expected value $ E[c(1)] $ : - $ P(c(1) = 0) = 0 $ , since $ c(1) $ is set to $ 1 $ from the start. - $ P(c(1) = 1) = \frac{1}{2} $ , since there is the only one series of moves that leads $ c(1) = 1 $ . It's $ 1 \rightarrow 2 \rightarrow 3 $ with probability $ 1 \cdot \frac{1}{2} $ . - $ P(c(1) = 2) = \frac{1}{4} $ : the only path is $ 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3 $ . - $ P(c(1) = 3) = \frac{1}{8} $ : the only path is $ 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3 $ . - $ P(c(1) = i) = \frac{1}{2^i} $ in general case. As a result, $ E[c(1)] = \sum\limits_{i=1}^{\infty}{i \frac{1}{2^i}} = 2 $ . Image of tree in second test 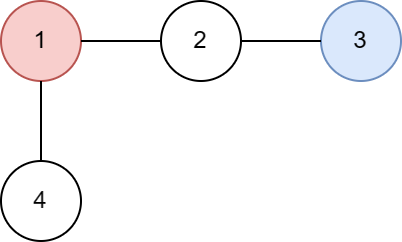 Image of tree in third test