CF1823F Random Walk

给定一棵包含 $n$ 个顶点和 $n-1$ 条边的树，每个顶点 $v$ 都有一个计数器 $c(v)$。 初始时，有一个棋子放在顶点 $s$，所有计数器都被设为 $0$，除了 $c(s)$ 被设为 $1$。 你的目标是将棋子移动到顶点 $t$。你可以通过一系列操作实现这一目标。假设当前棋子在顶点 $v$，每一步操作如下： 1. 从顶点 $v$ 的所有邻居中等概率随机选择一个顶点 $to$（如果存在边 $\{v, to\}$，则 $to$ 是 $v$ 的邻居）； 2. 将棋子移动到顶点 $to$，并将 $c(to)$ 增加 $1$； 你会重复上述操作，直到到达顶点 $t$。 对于每个顶点 $v$，计算 $c(v)$ 的期望值，并对 $998\,244\,353$ 取模。

第一行包含三个整数 $n$、$s$ 和 $t$（$2 \le n \le 2 \times 10^5$，$1 \le s, t \le n$，$s \neq t$），分别表示树的顶点数、起点和终点。 接下来的 $n-1$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$，$u_i \neq v_i$），表示树中的一条边。 保证所给边构成一棵树。

输出 $n$ 个数，依次表示每个顶点 $v$ 的 $c(v)$ 的期望值对 $998\,244\,353$ 取模的结果。 形式化地，设 $M = 998\,244\,353$。可以证明答案可以表示为最简分数 $\frac{p}{q}$，其中 $p$ 和 $q$ 是整数且 $q \not\equiv 0 \pmod{M}$。输出一个整数 $x$，满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod{M}$。

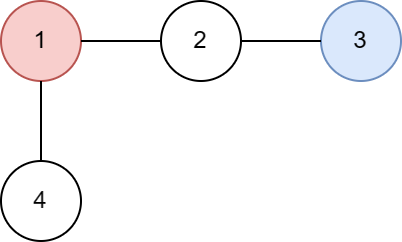
第一组样例的树如下图所示：  我们来计算 $E[c(1)]$ 的期望值： - $P(c(1) = 0) = 0$，因为 $c(1)$ 初始就被设为 $1$。 - $P(c(1) = 1) = \frac{1}{2}$，因为只有一种移动序列使 $c(1) = 1$，即 $1 \rightarrow 2 \rightarrow 3$，概率为 $1 \cdot \frac{1}{2}$。 - $P(c(1) = 2) = \frac{1}{4}$，唯一的路径是 $1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$。 - $P(c(1) = 3) = \frac{1}{8}$，唯一的路径是 $1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$。 - 一般情况下，$P(c(1) = i) = \frac{1}{2^i}$。 因此，$E[c(1)] = \sum\limits_{i=1}^{\infty}{i \frac{1}{2^i}} = 2$。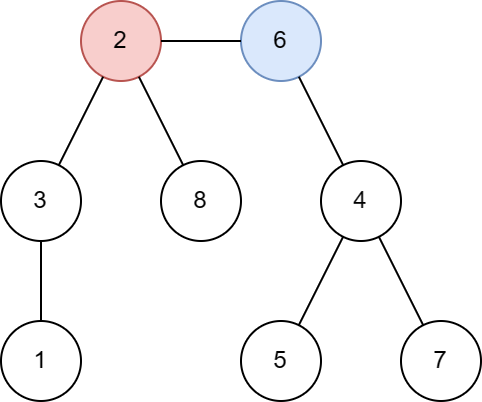 第二组样例的树结构如下图所示：  第三组样例的树结构如下图所示：  由 ChatGPT 4.1 翻译