CF1824B2 LuoTianyi and the Floating Islands (Hard Version)

这是该问题的困难版本。唯一的区别在于本版本中 $k \le n$。只有当你同时解决了该问题的两个版本时，才能进行 hack。  Chtholly 和浮空岛。LuoTianyi 现在生活在一个有 $n$ 个浮空岛的世界里。这些浮空岛通过 $n-1$ 条无向空中航线连接，任意两个岛屿都可以通过这些航线互相到达。也就是说，这 $n$ 个浮空岛构成了一棵树。 有一天，LuoTianyi 想去见她的朋友们：Chtholly、Nephren、William，等等。她一共想见 $k$ 个人。她不知道他们的具体位置，但她知道他们分别在 $k$ 个不同的岛屿上。她定义一个岛屿是“好”的，当且仅当从该岛屿到这 $k$ 个有人岛屿的距离之和，在所有 $n$ 个岛屿中最小。 现在，LuoTianyi 想知道，如果这 $k$ 个人随机分布在 $n$ 个岛屿中的 $k$ 个不同岛屿上，那么期望有多少个“好”岛屿？你只需要告诉她这个期望值对 $10^9+7$ 取模的结果。 $^\dagger$ 两个岛屿之间的距离是指从一个岛屿到另一个岛屿所需经过的最少航线数。

第一行包含两个整数 $n$ 和 $k$（$1 \le k \le n \le 2 \times 10^5$），分别表示岛屿数和人数。 接下来的 $n-1$ 行描述空中航线。第 $i$ 行包含两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n, u_i \neq v_i$），表示第 $i$ 条航线连接的两个岛屿。

输出一个整数，表示“好”岛屿的期望数量对 $10^9+7$ 取模的结果。 形式化地，设 $M = 10^9 + 7$。可以证明答案可以表示为最简分数 $\frac{p}{q}$，其中 $p$ 和 $q$ 是整数，且 $q \not\equiv 0 \pmod{M}$。请输出一个整数 $x$，满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod{M}$。

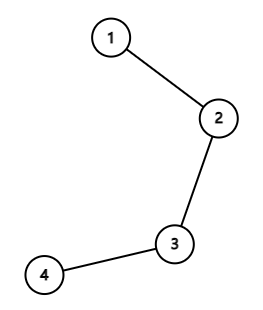
在第一个样例中，航线构成如下的树：  如果这两个人分别在岛屿 $1$ 和 $2$ 上，则岛屿 $1$ 和 $2$ 都是“好”岛屿。 从岛屿 $1$ 或 $2$ 到所有人的距离之和是 $1+0=1$，这是最小值。而从岛屿 $3$ 到所有人的距离之和是 $2+1=3$，大于 $1$。 类似地，当两个人在岛屿 $1$ 和 $3$ 时，岛屿 $1,2,3$ 都是“好”岛屿。 当两个人在岛屿 $1$ 和 $4$ 时，岛屿 $1,2,3,4$ 都是“好”岛屿。 当两个人在岛屿 $2$ 和 $3$ 时，岛屿 $2$ 和 $3$ 是“好”岛屿。 当两个人在岛屿 $2$ 和 $4$ 时，岛屿 $2,3,4$ 是“好”岛屿。 当两个人在岛屿 $3$ 和 $4$ 时，岛屿 $3$ 和 $4$ 是“好”岛屿。 所以“好”岛屿数量的期望为 $\frac{16}{6}$，对 $10^9+7$ 取模后等于 $666666674$。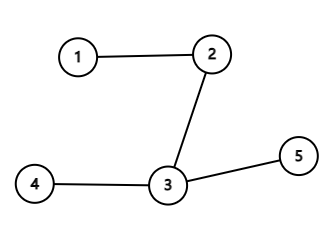 在第二个样例中，航线构成如下的树：  可以看到每个岛屿上各有一个人，只有岛屿 $3$ 是“好”岛屿。所以期望数量为 $1$。 由 ChatGPT 4.1 翻译