CF1824C LuoTianyi and XOR-Tree

LuoTianyi gives you a tree with values in its vertices, and the root of the tree is vertex $ 1 $ . In one operation, you can change the value in one vertex to any non-negative integer. Now you need to find the minimum number of operations you need to perform to make each path from the root to leaf $ ^{\dagger} $ has a [bitwise XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR) value of zero. $ ^{\dagger} $ A leaf in a rooted tree is a vertex that has exactly one neighbor and is not a root.

The first line contains a single integer $ n $ ( $ 2 \le n \le 10^5 $ ) — the number of vertices in the tree. The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le 10^9 $ ), the $ i $ -th number represents the value in the $ i $ -th vertex. Next $ n−1 $ lines describe the edges of the tree. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i,v_i \le n, u_i \neq v_i $ ) — the vertices connected by an edge of the tree. It's guaranteed that the given edges form a tree.

Print a single integer — the minimum number of operations.

The tree in the first example: 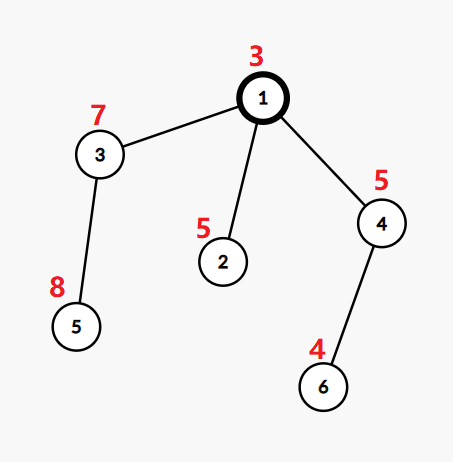 If we change the value in the vertex $ 2 $ to $ 3 $ , the value in the vertex $ 5 $ to $ 4 $ , and the value in the vertex $ 6 $ to $ 6 $ , then the tree will be ok. The bitwise XOR from the root to the leaf $ 2 $ will be $ 3 \oplus 3=0 $ . The bitwise XOR from the root to the leaf $ 5 $ will be $ 4 \oplus 7 \oplus 3=0 $ . The bitwise XOR from the root to the leaf $ 6 $ will be $ 6 \oplus 5 \oplus 3=0 $ . The tree in the second example: 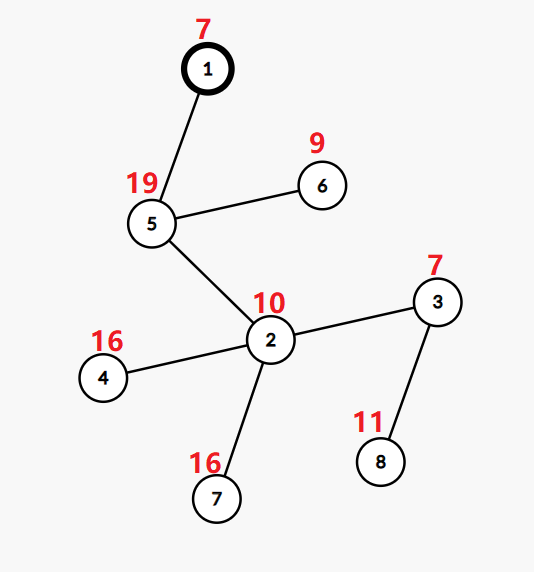 If we change the value in the vertex $ 2 $ to $ 4 $ , the value in the vertex $ 3 $ to $ 27 $ , and the value in the vertex $ 6 $ to $ 20 $ , then the tree will be ok. The bitwise XOR from the root to the leaf $ 6 $ will be $ 20 \oplus 19 \oplus 7=0 $ . The bitwise XOR from the root to the leaf $ 8 $ will be $ 11 \oplus 27 \oplus 4 \oplus 19 \oplus 7=0 $ . The bitwise XOR from the root to the leaf $ 4 $ will be $ 16 \oplus 4 \oplus 19 \oplus 7=0 $ . The bitwise XOR from the root to the leaf $ 7 $ will be $ 16 \oplus 4 \oplus 19 \oplus 7=0 $ . In the third example, the only leaf is the vertex $ 4 $ and the bitwise XOR on the path to it is $ 1 \oplus 2 \oplus 1 \oplus 2 = 0 $ , so we don't need to change values. In the fourth example, we can change the value in the vertex $ 1 $ to $ 5 $ , and the value in the vertex $ 4 $ to $ 0 $ . Here $ \oplus $ denotes the bitwise XOR operation.