CF1824C LuoTianyi and XOR-Tree

洛天依给你一棵树，树的每个顶点上都有一个值，树的根为顶点 $1$。 每次操作，你可以将某个顶点上的值更改为任意非负整数。 现在你需要求出，最少需要多少次操作，才能使得从根到每个叶子的路径上的所有值的按位异或（bitwise XOR）结果都为零。 $^\dagger$ 在有根树中，叶子是指恰好有一个邻居且不是根的顶点。

第一行包含一个整数 $n$（$2 \le n \le 10^5$），表示树的顶点数。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \le a_i \le 10^9$），其中第 $i$ 个数表示第 $i$ 个顶点上的值。 接下来的 $n-1$ 行描述树的边。第 $i$ 行包含两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n, u_i \neq v_i$），表示一条连接顶点 $u_i$ 和 $v_i$ 的边。保证给出的边构成一棵树。

输出一个整数，表示最少需要的操作次数。

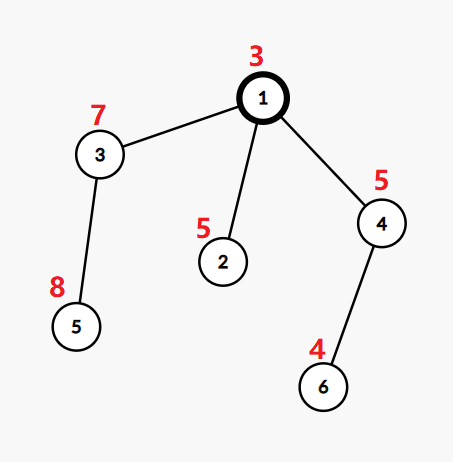
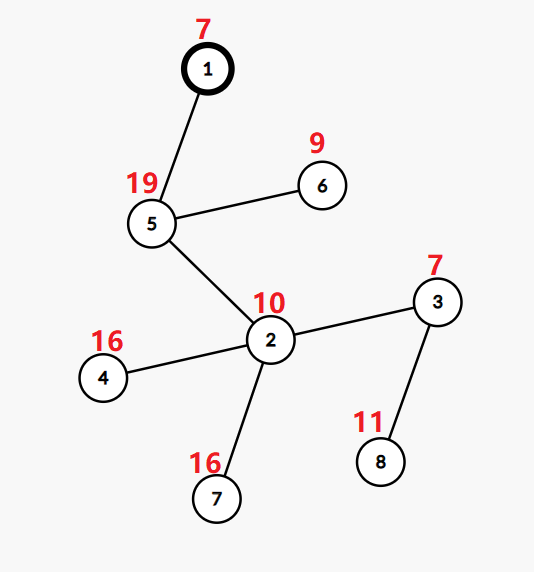
第一个样例中的树如下：  如果我们将顶点 $2$ 的值改为 $3$，顶点 $5$ 的值改为 $4$，顶点 $6$ 的值改为 $6$，那么这棵树就满足要求了。 从根到叶子 $2$ 的路径的异或值为 $3 \oplus 3 = 0$。 从根到叶子 $5$ 的路径的异或值为 $4 \oplus 7 \oplus 3 = 0$。 从根到叶子 $6$ 的路径的异或值为 $6 \oplus 5 \oplus 3 = 0$。 第二个样例中的树如下：  如果我们将顶点 $2$ 的值改为 $4$，顶点 $3$ 的值改为 $27$，顶点 $6$ 的值改为 $20$，那么这棵树就满足要求了。 从根到叶子 $6$ 的路径的异或值为 $20 \oplus 19 \oplus 7 = 0$。 从根到叶子 $8$ 的路径的异或值为 $11 \oplus 27 \oplus 4 \oplus 19 \oplus 7 = 0$。 从根到叶子 $4$ 的路径的异或值为 $16 \oplus 4 \oplus 19 \oplus 7 = 0$。 从根到叶子 $7$ 的路径的异或值为 $16 \oplus 4 \oplus 19 \oplus 7 = 0$。 第三个样例中，唯一的叶子是顶点 $4$，从根到它的路径异或值为 $1 \oplus 2 \oplus 1 \oplus 2 = 0$，因此无需更改任何值。 第四个样例中，我们可以将顶点 $1$ 的值改为 $5$，顶点 $4$ 的值改为 $0$。 这里的 $\oplus$ 表示按位异或操作。 由 ChatGPT 4.1 翻译