CF1824E LuoTianyi and Cartridge

给定一棵 $n$ 个结点的树 $T$，点有点权 $a_i, b_i$，边有边权 $c_i, d_i$。 按如下方式构建另一棵树 $T'$： - 选择 $T$ 的 $p$ 个结点作为 $T'$ 的点集 $V'$。$p$ 可以是 $1\sim n$ 的任意正整数。 - 接下来 **依次** 选择 $T$ 的 $p - 1$ 条 **互不相同** 的边。 - 对于第 $i$ 次选边，假设选择第 $j$ 条边 $(x_j, y_j)$，那么你可以选择 $V'$ 的 **不连通** 的两个点 $u, v$，要求 $(x_j, y_j)$ 包含于 $u, v$ 在 $T$ 上的简单路径，在 $u, v$ 之间以 $c_j, d_j$ 为权值连边。 设 $A, C$ 分别为 $T'$ 的 $a_i, c_i$ 的最小值，$B, D$ 分别为 $T'$ 的 $b_i, d_i$ 之和，则 $T'$ 的权值为 $\min(A, C)\cdot (B + D)$。 求 $T'$ 的最大权值。 $3\leq n\leq 2\times 10 ^ 5$，$1\leq a_i, b_i, c_i, d_i\leq 2\times 10 ^ 5$，保证 $(x_i, y_i)$ 形成一棵树。

第一行一个正整数 $n$。 第二行 $n$ 个正整数 $a_i$。 第三行 $n$ 个正整数 $b_i$。 接下来 $n - 1$ 行，每行四个正整数 $x_i, y_i, c_i, d_i$。

输出一行一个整数表示答案 —— $T'$ 的最大权值。 翻译提供者：[Alex_Wei](https://www.luogu.com.cn/user/123294)。

The tree from the first example is shown in the statement. The tree from the second example is shown below: 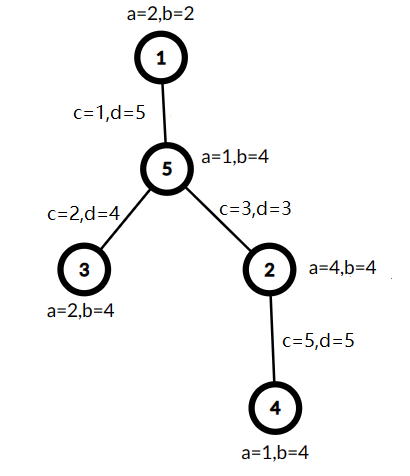 $ A = 1, B = 18, C = 1, D = 17 $ , so the cost is $ \min(1,1) \cdot (18 + 17) = 35 $ .