CF1824E LuoTianyi and Cartridge

LuoTianyi is watching the anime Made in Abyss. She finds that making a Cartridge is interesting. To describe the process of making a Cartridge more clearly, she abstracts the original problem and gives you the following problem. You are given a tree $ T $ consisting of $ n $ vertices. Each vertex has values $ a_i $ and $ b_i $ and each edge has values $ c_j $ and $ d_j $ . Now you are aim to build a tree $ T' $ as follows: - First, select $ p $ vertices from $ T $ ( $ p $ is a number chosen by yourself) as the vertex set $ S' $ of $ T' $ . - Next, select $ p-1 $ edges from $ T $ one by one (you cannot select one edge more than once). - May you have chosen the $ j $ -th edge connects vertices $ x_j $ and $ y_j $ with values $ (c_j,d_j) $ , then you can choose two vertices $ u $ and $ v $ in $ S' $ that satisfy the edge $ (x_j,y_j) $ is contained in the simple path from $ u $ to $ v $ in $ T $ , and link $ u $ and $ v $ in $ T' $ by the edge with values $ (c_j,d_j) $ ( $ u $ and $ v $ shouldn't be contained in one connected component before in $ T' $ ). 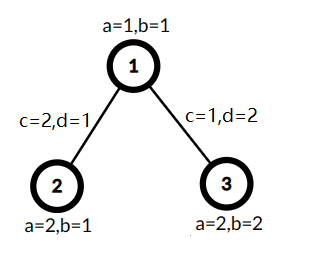 A tree with three vertices, $ \min(A,C)=1,B+D=7 $ , the cost is $ 7 $ . 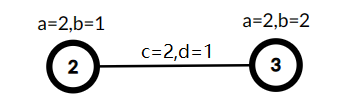 Selected vertices $ 2 $ and $ 3 $ as $ S' $ , used the edge $ (1,2) $ with $ c_j = 2 $ and $ d_j = 1 $ to link this vertices, now $ \min(A,C)=2,B+D=4 $ , the cost is $ 8 $ .Let $ A $ be the minimum of values $ a_i $ in $ T' $ and $ C $ be the minimum of values $ c_i $ in $ T' $ . Let $ B $ be the sum of $ b_i $ in $ T' $ and $ D $ be the sum of values $ d_i $ in $ T' $ . Let $ \min(A, C) \cdot (B + D) $ be the cost of $ T' $ . You need to find the maximum possible cost of $ T' $ .

The first line contains one integer $ n $ ( $ 3\le n \le 2\cdot 10^5 $ ) — the number of vertices in the tree $ T $ . The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1\le a_i\le 2\cdot 10^5 $ ), where the $ i $ -th integer represents the $ a_i $ value of the $ i $ -th vertex. The third line contains $ n $ integers $ b_1, b_2, \ldots, b_n $ ( $ 1\le b_i\le 2\cdot 10^5 $ ), where the $ i $ -th integer represents the $ b_i $ value of the $ i $ -th vertex. Then $ n-1 $ lines follow, the $ j $ -th of them contains four integers $ x_j,y_j,c_j,d_j $ ( $ 1\le x_j,y_j\le n,1\le c_j,d_j\le 2\cdot 10^5 $ ) representing the edge $ (x_j,y_j) $ and its values $ c_j $ and $ d_j $ respectively. It's guaranteed that edges form a tree.

Print a single integer — the maximum possible cost of $ T' $ .

The tree from the first example is shown in the statement. The tree from the second example is shown below: 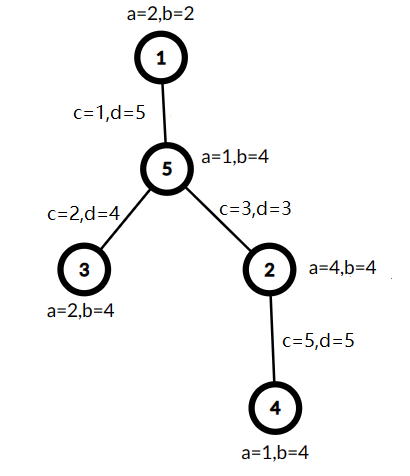 $ A = 1, B = 18, C = 1, D = 17 $ , so the cost is $ \min(1,1) \cdot (18 + 17) = 35 $ .