CF1826F Fading into Fog

这是一个交互题。 在二维欧几里得平面上有 $n$ 个不同的隐藏点，坐标为实数。在一次询问中，你可以指定一条直线 $ax + by + c = 0$，并获得所有 $n$ 个点在这条直线上的投影，顺序任意。注意，给出的投影并不是完全精确的，具体请阅读交互部分。 请用最少的询问次数，猜出所有 $n$ 个点，并以任意顺序输出它们。这里的“最少”指的是解决任意可能的 $n$ 个点的测试用例所需的最小询问次数。 隐藏点在交互过程中是固定的，不会发生变化。换句话说，交互器不是自适应的。 点 $A$ 到直线 $ax + by + c = 0$ 的投影是 $A$ 到该直线距离最近的点。

第一行包含一个整数 $t$（$1 \leq t \leq 50$）——表示测试用例的数量。 每个测试用例的描述如下。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 25$）——表示隐藏点的数量。 保证对于任意一对隐藏点，它们的 $x$ 坐标至少相差 $1$，同理，$y$ 坐标也至少相差 $1$。 所有隐藏点的 $x$ 和 $y$ 坐标的绝对值都不超过 $100$。

每次询问一条直线 $ax + by + c = 0$ 时，你应输出 "? a b c"，其中 $a$、$b$、$c$ 均为绝对值不超过 $100$ 的实数。为减少精度问题，$a$ 和 $b$ 必须满足 $|a| + |b| \geq 0.1$，其中 $|a|$ 表示 $a$ 的绝对值。 对于每次询问，你将获得 $n$ 个点，格式为 "x\_1 y\_1 ... x\_n y\_n"，其中点 $(x_i, y_i)$ 是投影到直线 $ax + by + c = 0$ 上的点。保证每个输出点距离真实投影点不超过 $10^{-4}$。每个坐标最多保留 9 位小数。 具体交互样例见下文。 如果你询问次数过多，将会收到 Wrong answer。 输出答案时，应输出 "! x\_1 y\_1 ... x\_n y\_n"，其中 $(x_i, y_i)$ 是隐藏点的坐标，顺序任意。如果你输出的每个点距离真实隐藏点不超过 $10^{-3}$，则答案被认为是正确的。输出答案不计入询问次数。 每次输出询问或答案后，别忘了输出换行并刷新输出缓冲区，否则会收到 Idleness limit exceeded。具体操作如下： - C++：fflush(stdout) 或 cout.flush() - Java：System.out.flush() - Pascal：flush(output) - Python：stdout.flush() - 其它语言请查阅相关文档 Hack 制作 Hack 时，使用如下格式： 第一行输出一个整数 $t$（$1 \leq t \leq 50$）——表示测试用例数量。 每个测试用例的描述如下。 每个测试用例的第一行输出一个整数 $n$（$2 \leq n \leq 25$）。接下来的 $n$ 行，每行输出两个有理数，分别为 $x_i$ 和 $y_i$。每个点都应满足输入部分的所有约束。

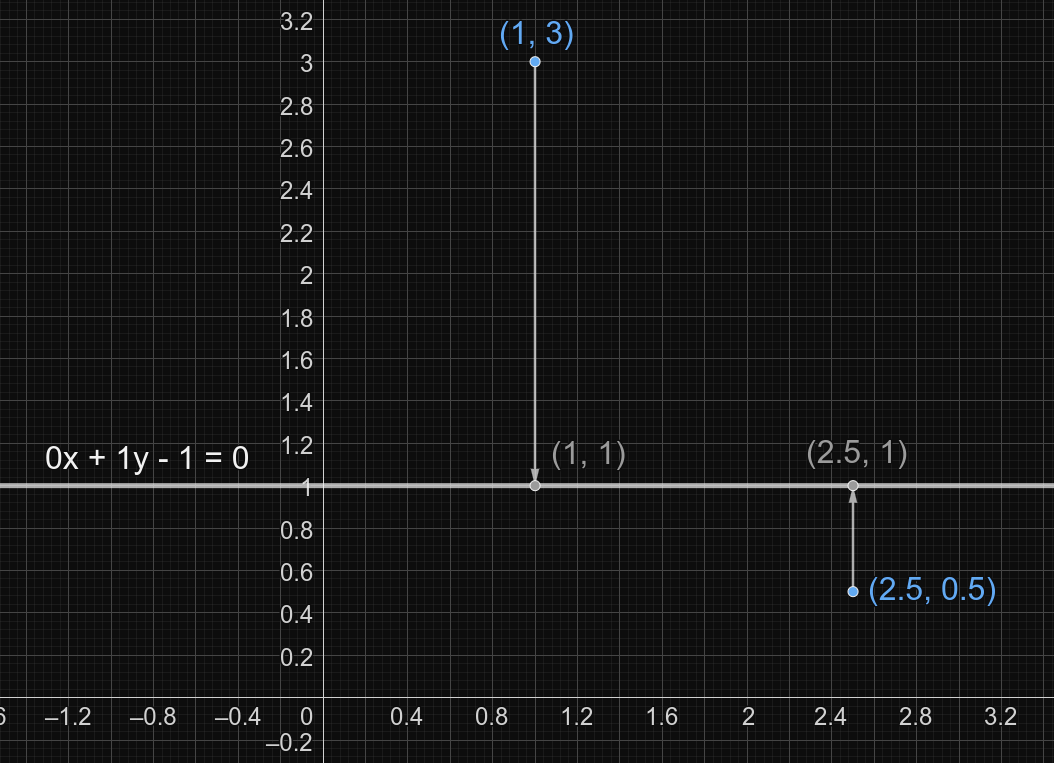
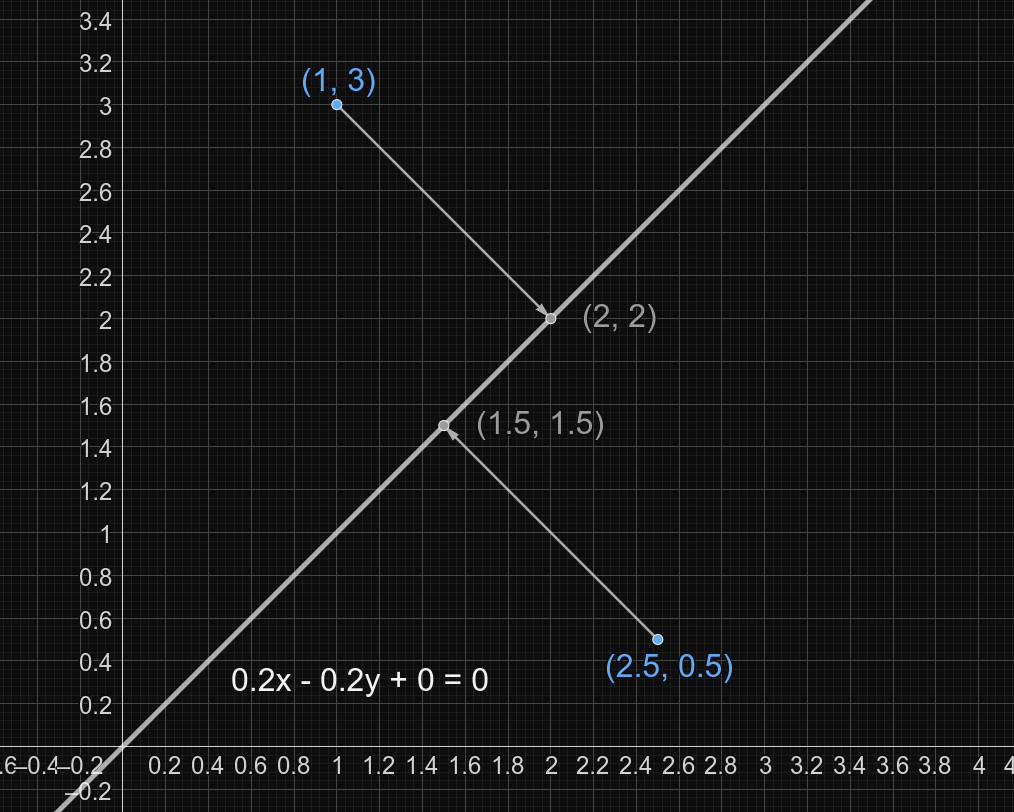
在样例中，隐藏点为 $(1, 3)$ 和 $(2.5, 0.5)$。 下图描述了第一次询问的情形：  下图描述了第二次询问的情形：  由 ChatGPT 4.1 翻译