CF1827D Two Centroids
题目描述
给定一棵树(无向连通无环图),初始时仅包含顶点 $1$。接下来会有若干次操作。在第 $i$ 次操作中,顶点 $i+1$ 会出现,并与顶点 $p_i$($1 \le p_i \le i$)相连。
每次操作后,请你求出最少需要多少次操作,才能使当前的树拥有两个重心。每次操作可以向树中添加一个顶点和一条边,且添加后仍然是一棵树。
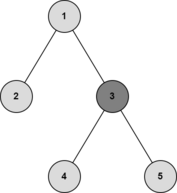
如果移除某个顶点后,所有连通块的大小都不超过 $\lfloor \frac{n}{2} \rfloor$($n$ 为树的顶点数),则该顶点称为树的重心。例如,下图中,顶点 $3$ 是重心,因为移除 $3$ 后最大的连通块大小为 $2$。
在下图中,顶点 $1$ 和 $2$ 都是重心。
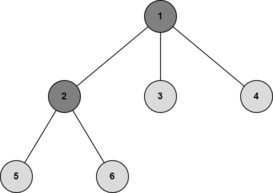
输入格式
每组测试数据包含多组测试用例。第一行包含一个整数 $t$($1 \le t \le 10^4$),表示测试用例的组数。
每组测试用例的第一行包含一个整数 $n$($2 \le n \le 5 \cdot 10^{5}$),表示最终树的节点数。
第二行包含 $n-1$ 个整数 $p_1, p_2, \ldots, p_{n-1}$($1 \le p_i \le i$),表示第 $i+1$ 个顶点连接到的顶点编号。
保证所有测试用例中 $n$ 的总和不超过 $5 \cdot 10^{5}$。
输出格式
对于每组测试用例,输出 $n-1$ 个整数,第 $i$ 个整数表示第 $i$ 次操作后,使当前树拥有两个重心所需的最少操作次数。
可以证明答案总是存在。
说明/提示
下图为第四个样例测试用例的说明。
第三次操作后:
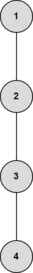
此时树已经有顶点 $2$ 和 $3$ 作为重心,因此不需要操作。
第四次操作后:
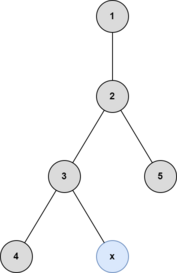
添加顶点 $x$ 后,顶点 $2$ 和 $3$ 成为重心。只需一次操作。
第五次操作后:
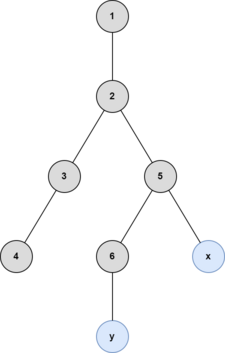
添加顶点 $x$ 和 $y$ 后,顶点 $5$ 和 $2$ 成为重心。需要两次操作。
第六次操作后:
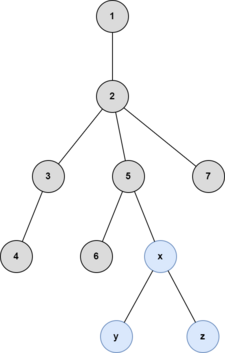
添加顶点 $x$、$y$ 和 $z$ 后,顶点 $5$ 和 $2$ 成为重心。需要三次操作。
由 ChatGPT 4.1 翻译