CF1829F Forever Winter

A snowflake graph is generated from two integers $ x $ and $ y $ , both greater than $ 1 $ , as follows: - Start with one central vertex. - Connect $ x $ new vertices to this central vertex. - Connect $ y $ new vertices to each of these $ x $ vertices. For example, below is a snowflake graph for $ x=5 $ and $ y=3 $ . 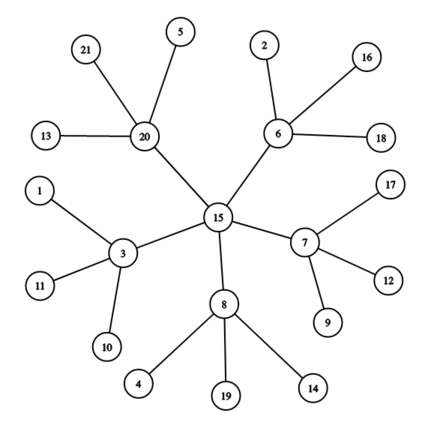The snowflake graph above has a central vertex $ 15 $ , then $ x=5 $ vertices attached to it ( $ 3 $ , $ 6 $ , $ 7 $ , $ 8 $ , and $ 20 $ ), and then $ y=3 $ vertices attached to each of those. Given a snowflake graph, determine the values of $ x $ and $ y $ .

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 1000 $ ) — the number of test cases. The first line of each test case contains two integers $ n $ and $ m $ ( $ 2 \leq n \leq 200 $ ; $ 1 \leq m \leq \min\left(1000, \frac{n(n-1)}{2}\right) $ ) — the number of vertices and edges in the graph, respectively. The next $ m $ lines each contain two integers each $ u $ and $ v $ ( $ 1 \leq u, v \leq n $ , $ u \neq v $ ) — the numbers of vertices connected by an edge. The graph does not contain multiple edges and self-loops. It is guaranteed that this graph is a snowflake graph for some integers $ x $ and $ y $ both greater than $ 1 $ .

For each test case, on a separate line output the values of $ x $ and $ y $ , in that order, separated by a space.

The first test case is pictured in the statement. Note that the output 3 5 is incorrect, since $ x $ should be output before $ y $ .