CF1829G Hits Different

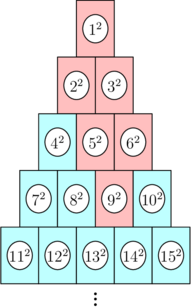
在一个嘉年华游戏中，有一个巨大的易拉罐金字塔，共有 $2023$ 行，编号方式如图所示。  如果最初击中编号为 $9^2$ 的易拉罐，那么图中所有红色的易拉罐都会倒下。 你向金字塔扔一个球，球击中了编号为 $n^2$ 的易拉罐。这会导致所有堆叠在该易拉罐上方的易拉罐都倒下（即，$n^2$ 号罐倒下，然后直接在其上方的罐也倒下，再然后是再上方的罐，依此类推）。例如，上图展示了击中 $9^2$ 号罐时会倒下的所有罐。 请问所有倒下的易拉罐编号之和是多少？注意，$n^2 = n \times n$。

第一行包含一个整数 $t$（$1 \leq t \leq 1000$），表示测试用例的数量。 每个测试用例占一行，包含一个整数 $n$（$1 \leq n \leq 10^6$），表示你击中的易拉罐编号为 $n^2$。

对于每个测试用例，输出一个整数，表示所有倒下的易拉罐编号之和。 请注意，对于某些测试用例，答案可能无法用 32 位整数类型存储，因此你应当在你的编程语言中使用至少 64 位整数类型（如 C++ 的 long long）。对于所有有效输入，答案都能用 64 位整数类型存储。

第一个测试用例如题面所示。所有倒下的易拉罐编号之和为 $1^2 + 2^2 + 3^2 + 5^2 + 6^2 + 9^2 = 1 + 4 + 9 + 25 + 36 + 81 = 156$。第二个测试用例中，只有编号为 $1^2$ 的罐倒下，所以答案是 $1^2=1$。第三个测试用例中，编号为 $1^2$ 和 $2^2$ 的罐倒下，所以答案是 $1^2+2^2=1+4=5$。第四个测试用例中，编号为 $1^2$ 和 $3^2$ 的罐倒下，所以答案是 $1^2+3^2=1+9=10$。第五个测试用例中，编号为 $1^2$、$2^2$ 和 $4^2$ 的罐倒下，所以答案是 $1^2+2^2+4^2=1+4+16=21$。 由 ChatGPT 4.1 翻译