CF1834F Typewriter
题目描述
# 打字机
最近,Polycarp收到了一台特殊的打字机作为礼物!不幸的是,这台打字机有一个相当奇怪的设计。
这台打字机由 $n$ 个单元组成,从左到右编号为 $1$ 到 $n$ ,还有一个移动的小车。打字机的每个单元包含 $n$ 个不同的整数,从 $1$ 到 $n$ ,每个单元 $i$ 最初包含整数 $p_i$ 。在所有操作之前,小车位于第一个单元上,它的缓冲区没有任何内容。当前小车所在的单元称为当前单元。
小车可以执行以下五种操作:
- 如果当前单元不为空,就将其中的整数放入小车的缓冲区(缓冲区最多只能容纳一个整数)。
- 如果小车的缓冲区不为空,就将其中的整数放入当前单元(如果当前单元为空)。
- 如果小车的缓冲区和当前单元都含有整数,就交换缓冲区中的整数和当前单元中的整数。
- 将小车从当前单元 $i$ 移动到下一个单元 $i+1$ (如果 $i
输入格式
第一行包含一个整数 $n$ ( $1 \le n \le 4 \cdot 10^5$ )——单元的数量。
第二行包含 $n$ 个不同的整数 $p_1, p_2, \ldots, p_n$ ( $1 \le p_i \le n$ )——单元中整数的初始排列。
第三行包含一个整数 $q$ ( $0 \le q \le 4 \cdot 10^5$ )——Polycarp提出的查询数量。
接下来的 $q$ 行描述了Polycarp的查询:
第 $j$ 行首先包含整数 $t_j$ ( $1 \le t_j \le 3$ )——查询的类型。
如果查询的类型是 $t_j = 1$ 或 $t_j = 2$ ,则在同一行中还会跟着整数 $k_j$ ( $1 \le k_j \le n$ )——移动的长度。
输出格式
输出 $q+1$ 个整数——在每个Polycarp的查询之前和之后,需要进行小车重置的最小次数。
## 样例 #1
### 样例输入 #1
```
3
2 3 1
0
```
### 样例输出 #1
```
1
```
## 样例 #2
### 样例输入 #2
```
3
1 2 3
2
2 1
3
```
### 样例输出 #2
```
0
2
1
```
## 样例 #3
### 样例输入 #3
```
5
3 1 2 5 4
5
1 3
3
2 3
1 4
3
```
### 样例输出 #3
```
3
2
1
2
1
2
```
说明/提示
在第一个示例中,答案为 $1$ 。你可以通过这个示例了解小车的工作方式。
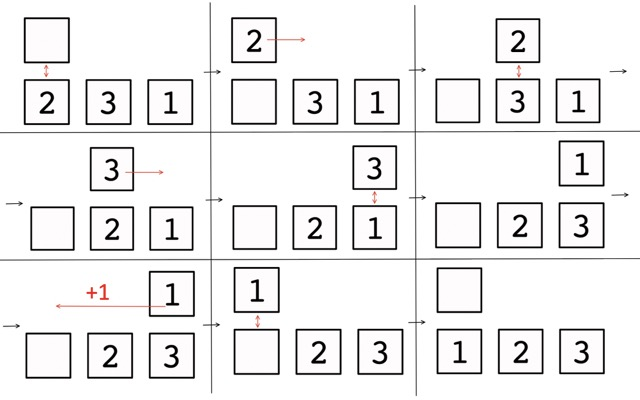在第二个示例中,需要计算答案的序列如下:
1. 所有查询之前:$1\ 2\ 3$ —— 答案为 $0$ 。
2. 右移 $1$ 位之后:$3\ 1\ 2$ —— 答案为 $2$ 。
3. 反转序列之后:$2\ 1\ 3$ —— 答案为 $1$ 。
在第三个示例中,每个查询之前和之后的序列如下:
1. $3\ 1\ 2\ 5\ 4$ —— 答案为 $3$ 。
2. $5\ 4\ 3\ 1\ 2$ —— 答案为 $2$ 。
3. $2\ 1\ 3\ 4\ 5$ —— 答案为 $1$ 。
4. $3\ 4\ 5\ 2\ 1$ —— 答案为 $2$ 。
5. $1\ 3\ 4\ 5\ 2$ —— 答案为 $1$ 。
6. $2\ 5\ 4\ 3\ 1$ —— 答案为 $2$ 。