CF1837E Playoff Fixing

有 $2^k$ 支队伍参加淘汰赛。队伍编号从 $1$ 到 $2^k$，编号越小实力越强。因此，队伍 $1$ 最强，队伍 $2^k$ 最弱。编号小的队伍总能战胜编号大的队伍。 首先，所有队伍会进行种子排序。每支队伍会被分配一个唯一的 $1$ 到 $2^k$ 的种子编号，表示其在淘汰赛中的初始位置。 比赛共进行 $2^k-1$ 场。比赛规则如下：所有队伍按种子编号分组，种子 $1$ 对种子 $2$，种子 $3$ 对种子 $4$，依此类推（顺序严格如此），这一轮共进行 $2^{k-1}$ 场比赛。每场比赛失败的队伍被淘汰。 接下来只剩下 $2^{k-1}$ 支队伍。如果只剩一支队伍，则该队伍为冠军；否则，继续进行 $2^{k-2}$ 场比赛：第一场由“种子 $1$ 对种子 $2$”的胜者对阵“种子 $3$ 对种子 $4$”的胜者，第二场由“种子 $5$ 对种子 $6$”的胜者对阵“种子 $7$ 对种子 $8$”的胜者，依此类推。如此循环，直到只剩一支队伍。 比赛结束后，所有队伍根据被淘汰的轮次获得名次，具体如下： - 冠军获得第 $1$ 名； - 决赛被淘汰的队伍获得第 $2$ 名； - 两支半决赛被淘汰的队伍获得第 $3$ 名； - 所有四分之一决赛被淘汰的队伍获得第 $5$ 名； - 所有 1/8 决赛被淘汰的队伍获得第 $9$ 名，依此类推。 现在我们要“操控”比赛结果，具体要求如下： - 队伍 $1$（不是种子 $1$ 的队伍）获得第 $1$ 名； - 队伍 $2$ 获得第 $2$ 名； - 队伍 $3$ 和 $4$ 获得第 $3$ 名； - 队伍 $5$ 到 $8$ 获得第 $5$ 名，依此类推。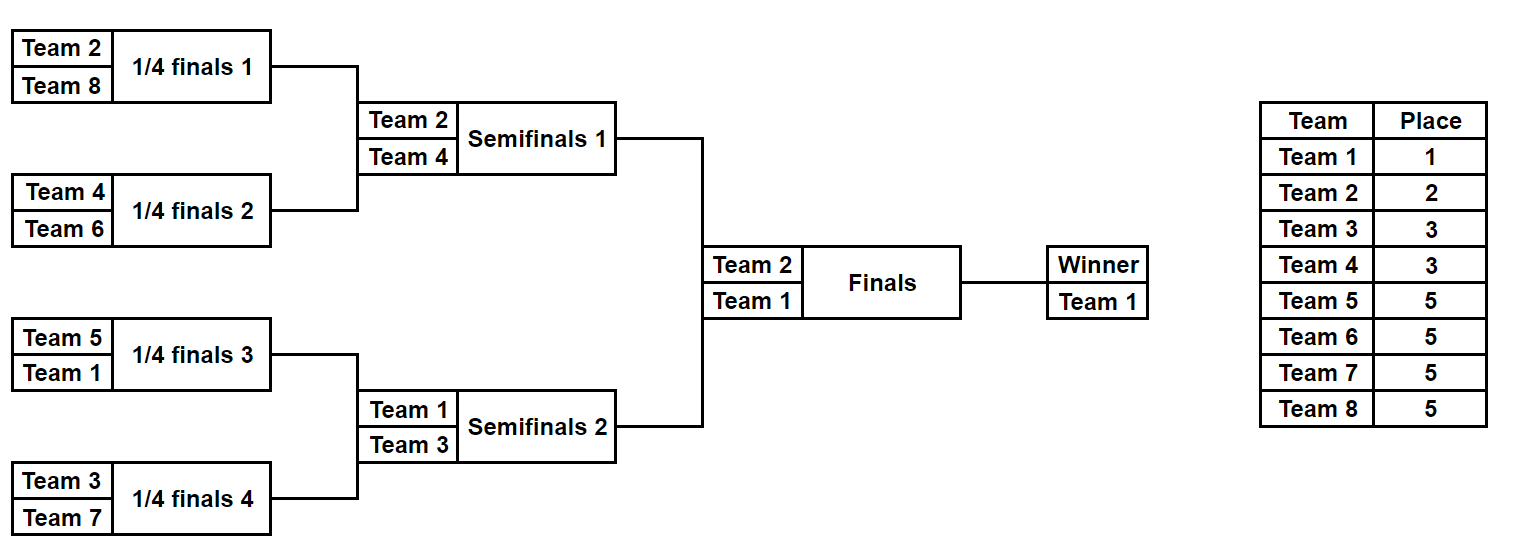 例如，下图展示了 $k=3$ 时比赛的一种可能安排及最终名次：  现在，部分种子编号已经被指定给了某些队伍（显然不止我们在操控比赛）。你需要将剩余的种子编号分配给剩余的队伍，使得最终名次如上所述。请问有多少种分配方案？由于答案可能很大，请输出对 $998\,244\,353$ 取模的结果。

第一行包含一个整数 $k$（$0 \le k \le 19$），表示有 $2^k$ 支队伍。 第二行包含 $2^k$ 个整数 $a_1, a_2, \dots, a_{2^k}$（$a_i = -1$ 或 $1 \le a_i \le 2^k$）。如果 $a_i \ne -1$，表示队伍 $a_i$ 被分配到了种子 $i$；否则，种子 $i$ 尚未分配给任何队伍。 所有非 $-1$ 的值互不相同。

输出一个整数，表示有多少种合法分配方案，使得比赛结果如题意所述，对 $998\,244\,353$ 取模。

由 ChatGPT 4.1 翻译