CF1838C No Prime Differences

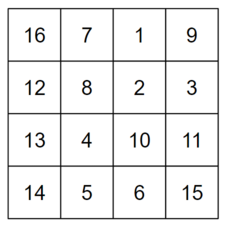
给定整数 $n$ 和 $m$，请用整数 $1$ 到 $n\cdot m$ 填充一个 $n$ 行 $m$ 列的网格，使得对于网格中任意两个相邻的格子，它们的值的绝对差不是质数。两个格子被认为是相邻的，当且仅当它们有公共边。  可以证明，在给定的约束条件下，总是存在解。

输入的第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。 接下来每个测试用例包含一行，包含两个整数 $n$ 和 $m$（$4 \le n, m \le 1000$），表示网格的行数和列数。 保证所有测试用例中 $n\cdot m$ 的总和不超过 $10^6$。

对于每个测试用例，输出 $n$ 行，每行 $m$ 个整数，表示最终的网格。每个数字 $1$ 到 $n\cdot m$ 恰好出现一次。 输出中多余的空格和空行仅用于便于阅读，不作要求。 如果存在多种方案，输出任意一种均可。

第一个样例对应上方的图片。该网格中所有相邻元素的绝对差为 $1$、$4$、$6$、$8$ 和 $9$，其中没有质数。 由 ChatGPT 4.1 翻译