CF1838F Stuck Conveyor

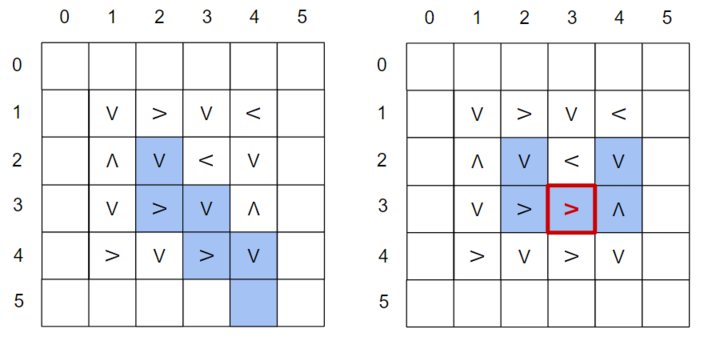
这是一个交互题。 在一个 $n \times n$ 的坐标平面上，$(1, 1)$ 到 $(n, n)$ 的位置上各有一个传送带。平面上的其他格子都是空的。每个传送带可以被设置为向上（`^`）、向下（`v`）、向左（``）移动箱子。如果箱子移动到一个空格子上，它就会停止移动。 然而，在这 $n^2$ 个传送带中，有一个传送带是卡住的，无论你如何设置，它总是会以同一个方向移动箱子。你的目标是通过一系列测试，确定哪个传送带卡住了，以及它的固定方向。 为此，你最多可以进行 $25$ 次测试。每次测试时，你可以为所有 $n^2$ 个传送带分配一个方向，在其中一个传送带上放置一个箱子，然后启动所有传送带。  这是 $n=4$ 时某次查询的可能结果。此时箱子从 $(2, 2)$ 出发。如果没有卡住的传送带，它最终会停在 $(5, 4)$，但由于 $(3, 3)$ 处的传送带卡住并向右（`>`），箱子进入了无限循环。 传送带移动箱子的速度太快，你无法看到过程，所以每次测试你只会得到箱子是否最终停止移动的信息，如果停止了，还会得到它最终的位置坐标。

你首先读取一个整数 $n$（$2 \le n \le 100$），表示网格的行数和列数。 接下来，你最多可以进行 $25$ 次查询。 每次查询应以一行 `? r c` 开始，$r$ 和 $c$ 分别表示箱子的初始行和列。 接下来的 $n$ 行，每行包含 $n$ 个字符，第 $i$ 行第 $j$ 个字符为 `^`、`v`、``，表示本次查询中 $(i, j)$ 处传送带的方向。 每次查询后，你会收到两个整数 $x$ 和 $y$。如果 $x = y = -1$，说明箱子进入了无限循环。否则，箱子最终停在 $(x, y)$。 如果你查询次数过多或查询格式非法，你将收到 Wrong Answer 判定。 在你确定卡住的传送带及其方向后，输出一行 `! r c dir`，其中 $r$ 和 $c$ 分别为卡住的传送带的行和列，`dir` 为其固定方向（`^`、`v`、``）。注意，输出这一行不计入 $25$ 次查询总数。输出后，程序应立即终止。 交互器是非自适应的。这意味着卡住的传送带的位置和方向在交互开始时就已确定，之后不会改变。 每次输出查询后不要忘记输出换行并刷新输出缓冲区，否则会收到 Idleness limit exceeded 判定。刷新方法如下： - C++：`fflush(stdout)` 或 `cout.flush()` - Java：`System.out.flush()` - Pascal：`flush(output)` - Python：`stdout.flush()` - 其他语言请查阅相关文档 Hack 格式 要制作 Hack，请使用以下格式： 第一行包含一个整数 $n$（$1 \le n \le 100$），表示网格的行数和列数。 第二行包含两个整数 $r$ 和 $c$（$1 \le r, c \le n$），以及一个字符 $\mathrm{dir}$（`^`、`v`、`` 之一），分别表示卡住的传送带的位置和固定方向。各值之间用空格分隔。

见输入格式说明。

对于第一个样例输入的第一次查询，箱子从 $(2, 2)$ 出发，进入了包含第 $2$ 行和第 $3$ 行的无限循环。由于卡住的传送带在第 $1$ 行，因此不会影响本次查询的结果。 对于第一个样例输入的第二次查询，传送带的配置与上一次相同，但箱子从 $(1, 1)$ 出发。如果没有卡住的传送带，它会在 $(1, 2)$ 和 $(1, 3)$ 之间无限循环。然而，卡住的传送带将其引向 $(0, 2)$。 通过这两次查询，程序可以确定卡住的传送带在 $(1, 2)$，且方向为向上（`^`）。 第二个样例输入的查询对应上图。查询后，卡住的传送带可能有多种可能，但程序正确地猜测它在 $(3, 3)$，方向为向右（`>`）。 由 ChatGPT 4.1 翻译