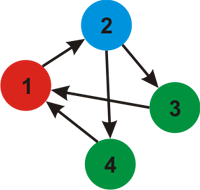
CF183C Cyclic Coloring

You are given a directed graph $ G $ with $ n $ vertices and $ m $ arcs (multiple arcs and self-loops are allowed). You have to paint each vertex of the graph into one of the $ k $ $ (k

The first line contains two space-separated integers $ n $ and $ m $ ( $ 1

Print a single integer — the maximum possible number of the colors that can be used to paint the digraph (i.e. $ k $ , as described in the problem statement). Note that the desired value of $ k $ must satisfy the inequality $ 1

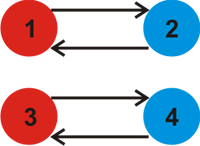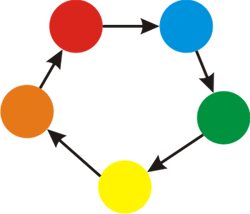
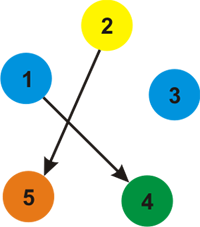For the first example, with $ k=2 $ , this picture depicts the two colors (arrows denote the next color of that color). With $ k=2 $ a possible way to paint the graph is as follows. It can be proven that no larger value for $ k $ exists for this test case. For the second example, here's the picture of the $ k=5 $ colors. A possible coloring of the graph is: For the third example, here's the picture of the $ k=3 $ colors. 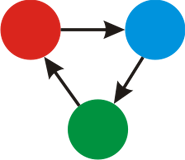A possible coloring of the graph is: