CF183C Cyclic Coloring
题目描述
给定一个有向图 $G$,包含 $n$ 个顶点和 $m$ 条有向边(允许重边和自环)。你需要使用 $k$ 种颜色($k \le n$)给图中的每个顶点进行染色,使得对于所有从顶点 $u$ 指向顶点 $v$ 的有向边,顶点 $v$ 必须被染为 $u$ 的下一个颜色。
颜色从 $1$ 到 $k$ 编号,且按照循环排列。这意味着对于每个颜色 $i$($i
输入格式
第一行包含两个用空格分隔的整数 $n$ 和 $m$($1 \le n, m \le 10^{5}$),表示该有向图的顶点数和有向边数。
接下来 $m$ 行,每行包含两个用空格分隔的整数 $a_i$ 和 $b_i$($1 \le a_i, b_i \le n$),表示第 $i$ 条边从顶点 $a_i$ 指向顶点 $b_i$。
允许重边和自环。
输出格式
输出一个整数,即可以用于染色该有向图的最大颜色数(即 $k$,如题目所述)。注意,$k$ 必须满足 $1 \le k \le n$。
说明/提示
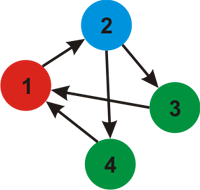
对于第一个样例,当 $k=2$ 时,图中两种颜色如图所示(箭头表示从当前颜色到下一种颜色的转移)。

当 $k=2$ 时,一种可行的染色方式如下。
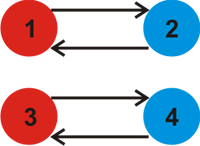
可以证明在本例中不存在更大的 $k$。
对于第二个样例,$k=5$ 时,各种颜色如图:
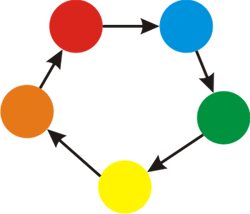
一种可行的染色如下:
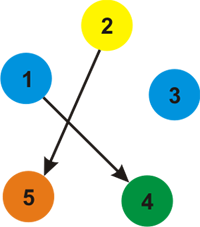
对于第三个样例,$k=3$ 时,各种颜色如图:
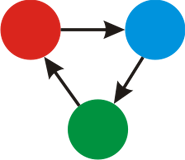
一种可行的染色如下:
由 ChatGPT 5 翻译