CF1842E Tenzing and Triangle
题目描述
在一个二维平面上有 $n$ 个两两不同的点和一条直线 $x+y=k$。第 $i$ 个点的坐标为 $(x_i, y_i)$。所有点的坐标都是非负数,并且严格在该直线下方。换句话说,$0 \leq x_i, y_i$,且 $x_i + y_i < k$。
Tenzing 想要擦除所有的点。他可以进行以下两种操作:
1. 画三角形:Tenzing 可以选择两个非负整数 $a$、$b$,满足 $a+b
输入格式
输入的第一行包含三个整数 $n$、$k$ 和 $A$($1 \leq n, k \leq 2 \times 10^5$,$1 \leq A \leq 10^4$)——点的数量、描述三角形斜边的系数以及画三角形的代价系数。
接下来的 $n$ 行,每行包含三个整数 $x_i, y_i, c_i$($0 \leq x_i, y_i, x_i + y_i < k$,$1 \leq c_i \leq 10^4$)——第 $i$ 个点的坐标以及用第二种操作擦除它的代价。保证所有点的坐标两两不同。
输出格式
输出一个整数,表示擦除所有点所需的最小代价。
说明/提示
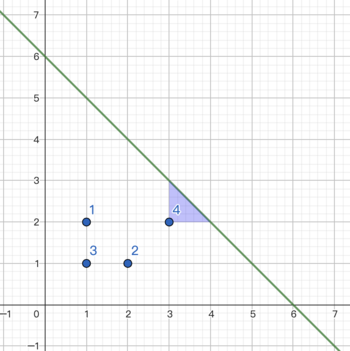
第一个样例的图示:
Tenzing 进行如下操作:
1. 画一个 $a=3, b=2$ 的三角形,代价 $=1 \cdot A=1$。
2. 擦除第一个点,代价 $=1$。
3. 擦除第二个点,代价 $=1$。
4. 擦除第三个点,代价 $=1$。
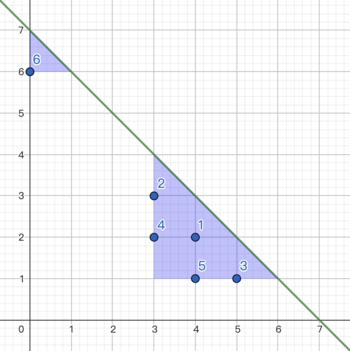
第二个样例的图示:
由 ChatGPT 4.1 翻译