CF1843D Apple Tree

Timofey 的花园里长着一棵苹果树，这是一棵有 $n$ 个结点的有根树，根节点为 $1$（结点编号从 $1$ 到 $n$）。树是一种无环且无重边的连通图。 这棵树非常特别——它是“根朝上”生长的。不过，对于程序员来说，这很正常。 苹果树还很年轻，所以只会长出两个苹果。苹果会长在某些结点上（这两个结点可以相同）。苹果长出来后，Timofey 会不断摇晃苹果树，直到苹果掉落。每次摇晃时，每个苹果会发生如下变化： 假设苹果当前在结点 $u$： - 如果结点 $u$ 有子结点，苹果会移动到其中一个子结点（如果有多个子结点，苹果可以移动到任意一个）。 - 否则，苹果会从树上掉落。 可以证明，经过有限次摇晃后，两个苹果都会掉落。 Timofey 有 $q$ 个关于苹果可能生长位置的假设。他假设苹果分别长在结点 $x$ 和 $y$，想知道有多少对结点 $(a, b)$，使得苹果分别从结点 $a$ 和 $b$ 掉落。请你帮他计算。

第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例数量。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 2 \times 10^5$），表示树的结点数。 接下来 $n-1$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1 \leq u_i, v_i \leq n$，$u_i \ne v_i$），表示树中的一条边。 接下来一行包含一个整数 $q$（$1 \leq q \leq 2 \times 10^5$），表示 Timofey 的假设数量。 接下来的 $q$ 行，每行包含两个整数 $x_i$ 和 $y_i$（$1 \leq x_i, y_i \leq n$），表示第 $i$ 个假设中苹果分别生长的结点。 保证所有测试用例中 $n$ 的总和不超过 $2 \times 10^5$，$q$ 的总和也不超过 $2 \times 10^5$。

对于每个 Timofey 的假设，输出一个整数，表示在该假设下，苹果分别从哪些结点掉落的有序对 $(a, b)$ 的数量。每个答案占一行。

在第一个样例中： - 对于第一个假设，有两种可能的掉落结点对：$(4, 4), (5, 4)$。 - 对于第二个假设，也有两种可能的对：$(5, 4), (5, 5)$。 - 对于第三个假设，只有一种可能的对：$(4, 4)$。 - 对于第四个假设，有 $4$ 种可能的对：$(4, 4), (4, 5), (5, 4), (5, 5)$。 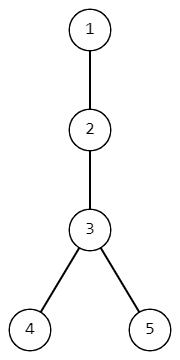 为第一个样例的树结构。 对于第二个样例，有 $4$ 种可能的掉落结点对：$(2, 3), (2, 2), (3, 2), (3, 3)$。对于第二个假设，只有一种可能的对：$(2, 3)$。对于第三个假设，有两种可能的对：$(3, 2), (3, 3)$。 由 ChatGPT 4.1 翻译