CF1846E2 Rudolf and Snowflakes (hard version)

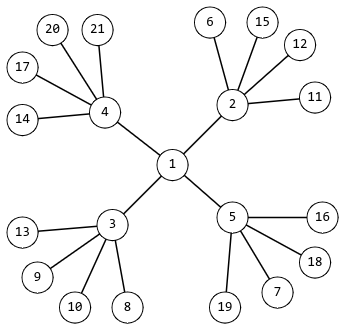
这是该问题的困难版本。唯一的区别在于本版本中 $n \le 10^{18}$。 一个冬日清晨，Rudolf 若有所思地望着窗外，观察着飘落的雪花。他很快注意到雪花的结构中存在某种对称性。作为一名真正的数学家，Rudolf 想出了一个雪花的数学模型。 他将雪花定义为按照以下规则构造的无向图： - 最初，图中只有一个顶点。 - 然后，向图中添加更多顶点。初始顶点通过边与 $k$ 个新顶点相连（$k > 1$）。 - 每个只与一个其他顶点相连的顶点，再通过边与 $k$ 个新顶点相连。此步骤至少要执行一次。 对于 $k=4$ 的最小雪花如下图所示。  经过一番数学研究，Rudolf 意识到，这样的雪花并不一定能拥有任意数量的顶点。请帮助 Rudolf 判断，是否存在一个雪花，其顶点数为 $n$。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 10^{18}$），表示需要判断是否存在顶点数为 $n$ 的雪花。

输出 $t$ 行，每行对应一个测试用例的答案——如果存在某个 $k > 1$，使得可以构造出顶点数为 $n$ 的雪花，则输出 "YES"；否则输出 "NO"。

由 ChatGPT 4.1 翻译