CF1850E Cardboard for Pictures

Mircea has $ n $ pictures. The $ i $ -th picture is a square with a side length of $ s_i $ centimeters. He mounted each picture on a square piece of cardboard so that each picture has a border of $ w $ centimeters of cardboard on all sides. In total, he used $ c $ square centimeters of cardboard. Given the picture sizes and the value $ c $ , can you find the value of $ w $ ? 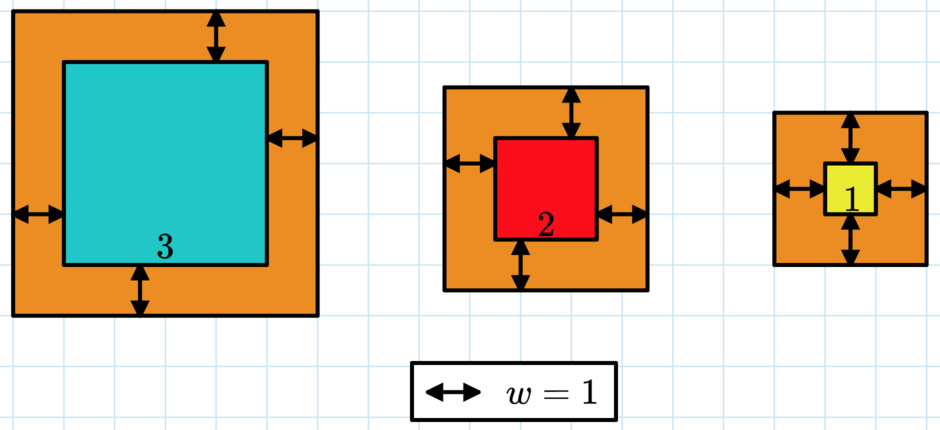 A picture of the first test case. Here $ c = 50 = 5^2 + 4^2 + 3^2 $ , so $ w=1 $ is the answer.Please note that the piece of cardboard goes behind each picture, not just the border.

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 1000 $ ) — the number of test cases. The first line of each test case contains two positive integers $ n $ ( $ 1 \leq n \leq 2 \cdot 10^5 $ ) and $ c $ ( $ 1 \leq c \leq 10^{18} $ ) — the number of paintings, and the amount of used square centimeters of cardboard. The second line of each test case contains $ n $ space-separated integers $ s_i $ ( $ 1 \leq s_i \leq 10^4 $ ) — the sizes of the paintings. The sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^5 $ . Additional constraint on the input: Such an integer $ w $ exists for each test case. Please note, that some of the input for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).

For each test case, output a single integer — the value of $ w $ ( $ w \geq 1 $ ) which was used to use exactly $ c $ squared centimeters of cardboard.

The first test case is explained in the statement. For the second test case, the chosen $ w $ was $ 2 $ , thus the only cardboard covers an area of $ c = (2 \cdot 2 + 6)^2 = 10^2 = 100 $ squared centimeters. For the third test case, the chosen $ w $ was $ 4 $ , which obtains the covered area $ c = (2 \cdot 4 + 2)^2 \times 5 = 10^2 \times 5 = 100 \times 5 = 500 $ squared centimeters.