CF1856E2 PermuTree (hard version)

这是该问题的困难版本。两个版本的区别在于 $n$ 的约束和时间限制。只有在两个版本都被解决的情况下，你才能进行 Hack。 给定一棵以顶点 $1$ 为根的 $n$ 个顶点的树。 对于长度为 $n$ 的某个排列 $^\dagger$ $a$，定义 $f(a)$ 为满足 $a_u < a_{\operatorname{lca}(u, v)} < a_v$ 的顶点对 $(u, v)$ 的数量。这里，$\operatorname{lca}(u,v)$ 表示顶点 $u$ 和 $v$ 的最近公共祖先。 请你求出所有长度为 $n$ 的排列 $a$ 中，$f(a)$ 的最大可能值。 $^\dagger$ 长度为 $n$ 的排列是一个包含 $1$ 到 $n$ 的 $n$ 个不同整数的数组，顺序任意。例如，$[2,3,1,5,4]$ 是一个排列，但 $[1,2,2]$ 不是排列（$2$ 在数组中出现了两次），$[1,3,4]$ 也不是排列（$n=3$ 但数组中有 $4$）。

第一行包含一个整数 $n$（$2 \le n \le 10^6$）。 第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$（$1 \le p_i < i$），表示存在一条连接顶点 $i$ 和 $p_i$ 的边。

输出 $f(a)$ 的最大值。

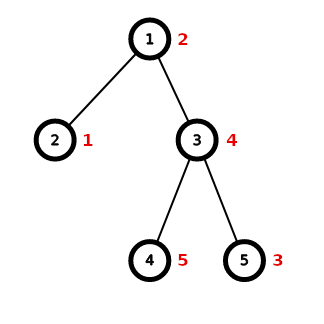
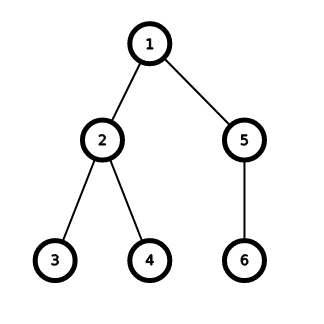
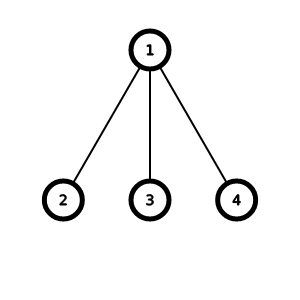
第一个测试中的树结构如下：  一种可能的最优排列 $a$ 为 $[2, 1, 4, 5, 3]$，此时有 $4$ 个满足条件的顶点对： - $(2, 3)$，因为 $\operatorname{lca}(2, 3) = 1$ 且 $1 < 2 < 4$； - $(2, 4)$，因为 $\operatorname{lca}(2, 4) = 1$ 且 $1 < 2 < 5$； - $(2, 5)$，因为 $\operatorname{lca}(2, 5) = 1$ 且 $1 < 2 < 3$； - $(5, 4)$，因为 $\operatorname{lca}(5, 4) = 3$ 且 $3 < 4 < 5$。 第三个测试中的树结构如下：  第四个测试中的树结构如下：  由 ChatGPT 4.1 翻译