CF1857D Strong Vertices

Given two arrays $ a $ and $ b $ , both of length $ n $ . Elements of both arrays indexed from $ 1 $ to $ n $ . You are constructing a directed graph, where edge from $ u $ to $ v $ ( $ u\neq v $ ) exists if $ a_u-a_v \ge b_u-b_v $ . A vertex $ V $ is called strong if there exists a path from $ V $ to all other vertices. A path in a directed graph is a chain of several vertices, connected by edges, such that moving from the vertex $ u $ , along the directions of the edges, the vertex $ v $ can be reached. Your task is to find all strong vertices. For example, if $ a=[3,1,2,4] $ and $ b=[4,3,2,1] $ , the graph will look like this: 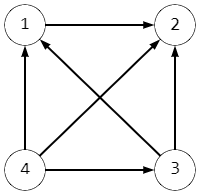 The graph has only one strong vertex with number $ 4 $

The first line contains an integer $ t $ ( $ 1\le t\le 10^4 $ ) — the number of test cases. The first line of each test case contains an integer $ n $ ( $ 2 \le n \le 2\cdot 10^5 $ ) — the length of $ a $ and $ b $ . The second line of each test case contains $ n $ integers $ a_1,a_2 \dots a_n $ ( $ -10^9 \le a_i \le 10^9 $ ) — the array $ a $ . The third line of each test case contains $ n $ integers $ b_1,b_2 \dots b_n $ ( $ -10^9 \le b_i \le 10^9 $ ) — the array $ b $ . It is guaranteed that the sum of $ n $ for all test cases does not exceed $ 2\cdot 10^5 $ .

For each test case, output two lines: in the first line, output the number of strong vertices, and in the second line, output all strong vertices in ascending order.

The first sample is covered in the problem statement. For the second sample, the graph looks like this: 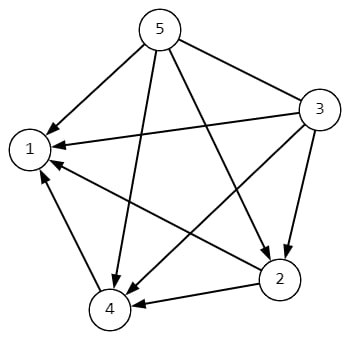 The graph has two strong vertices with numbers $ 3 $ and $ 5 $ . Note that there is a bidirectional edge between vertices $ 3 $ and $ 5 $ .In the third sample, the vertices are connected by a single directed edge from vertex $ 2 $ to vertex $ 1 $ , so the only strong vertex is $ 2 $ . In the fourth sample, all vertices are connected to each other by bidirectional edges, so there is a path from every vertex to any other vertex.