CF1857G Counting Graphs
题目描述
给定一棵包含 $n$ 个顶点的树。树是一个无环的连通无向图。树上的每条边都有一个权值 $w_i$。
你的任务是计算满足以下四个条件的不同图的数量:
1. 图中没有自环和重边。
2. 图中所有边的权值都是不超过 $S$ 的整数。
3. 图的最小生成树恰好有且只有一棵。
4. 图的最小生成树就是给定的这棵树。
如果两张图的边集不同(包括边的权值),则认为它们是不同的图。
答案可能很大,请输出对 $998244353$ 取模后的结果。
输入格式
第一行包含一个整数 $t$($1\le t\le 10^4$),表示测试用例的数量。
每个测试用例的第一行包含两个整数 $n$ 和 $S$($2 \le n \le 2 \cdot 10^5, 1\le S\le 10^9$),分别表示顶点数和权值上限。
接下来 $n-1$ 行描述这棵树,第 $i$ 行包含三个整数 $u_i$、$v_i$ 和 $w_i$($1\le u_i,v_i\le n, u_i \ne v_i, 1\le w_i\le S$),表示树中的一条边及其权值。
保证所有测试用例中 $n$ 的总和不超过 $2\cdot 10^5$。
输出格式
对于每个测试用例,输出满足条件的不同图的数量,对 $998244353$ 取模。
说明/提示
在第一个样例中,只有一张图,就是给定的树。
在第二个样例中,给定的树如下图所示:

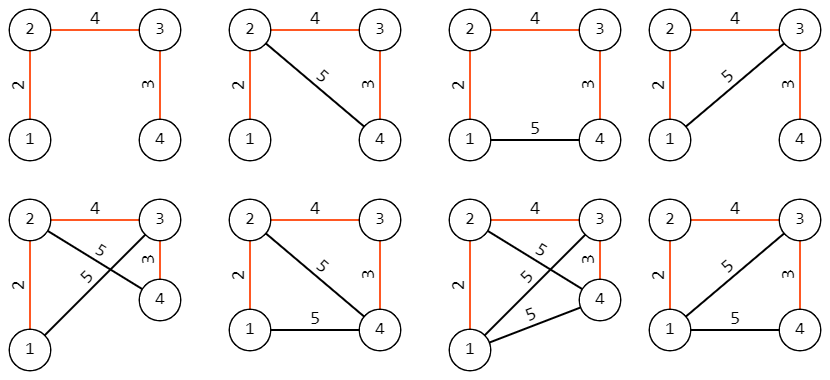
第二个样例的所有可能的图如下,最小生成树用红色高亮显示:
由 ChatGPT 4.1 翻译