CF1859D Andrey and Escape from Capygrad
题目描述
在 Tyagoland 的首都 Capygrad 发生了一起事件,城里的所有水豚都疯狂了,开始扔橘子。Andrey 被迫利用传送门尽可能远地逃离这座城市。
Tyagoland 被表示为一条数轴,Capygrad 位于 $0$ 点。全境共有 $n$ 个传送门,每个传送门由四个整数 $l_i$、$r_i$、$a_i$ 和 $b_i$($1 \le l_i \le a_i \le b_i \le r_i \le 10^9$)描述。注意,区间 $[a_i, b_i]$ 包含在区间 $[l_i, r_i]$ 内。
如果 Andrey 处于区间 $[l_i, r_i]$ 上,则该传送门可以将他传送到区间 $[a_i, b_i]$ 上的任意一点。Andrey 有一张通行证,可以无限次使用传送门。
Andrey 认为,当且仅当 $l \le x \le r$ 时,点 $x$ 在区间 $[l, r]$ 上。
Andrey 有 $q$ 个逃跑的起始选项,每个选项由一个整数 $x_i$ 表示——即第 $i$ 个选项的起始位置。他想要尽可能远离 Capygrad(即到达坐标最大的点)。请你帮助 Andrey 计算,从每个起始位置出发,他最多能逃到多远。
输入格式
每组测试数据包含多个测试用例。第一行包含一个整数 $t$($1 \le t \le 10^4$)——测试用例组数。接下来是每组测试用例的描述。
每组测试用例的第一行包含一个整数 $n$($1 \le n \le 2 \cdot 10^5$)——传送门的数量。
接下来的 $n$ 行,每行包含四个整数 $l_i$、$r_i$、$a_i$ 和 $b_i$($1 \le l_i \le a_i \le b_i \le r_i \le 10^9$)——传送门的参数。
接下来一行包含一个整数 $q$($1 \le q \le 2 \cdot 10^5$)——起始位置的数量。
下一行包含 $q$ 个整数 $x_1, x_2, \ldots, x_q$($1 \le x_i \le 10^9$)——Andrey 在第 $i$ 个选项中的起始位置。
保证所有测试用例中 $n$ 的总和与 $q$ 的总和均不超过 $2 \cdot 10^5$。
输出格式
对于每组测试用例,输出一行 $q$ 个整数,表示 Andrey 对每个起始位置的最优逃跑距离。
说明/提示
在第一个测试用例中:
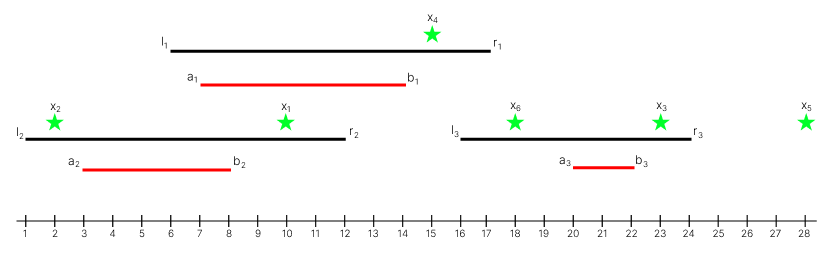
每个起始点的最优操作如下:
1. 使用传送门 $1$,传送到点 $b_1 = 14$。
2. 先使用传送门 $2$,传送到点 $6$,该点位于区间 $[l_1, r_1] = [6, 17]$,然后再用传送门 $1$,传送到点 $b_1 = 14$。
3. 停留在 $x_3=23$,不使用任何传送门。
4. 停留在 $x_4=15$,不使用任何传送门。
5. $x_5=28$ 不在任何区间内,Andrey 无法传送。
6. $x_6=18$ 只在区间 $[l_3, r_3] = [16, 24]$ 内,使用传送门 $3$,传送到点 $b_3 = 22$。
在第五个测试用例中:
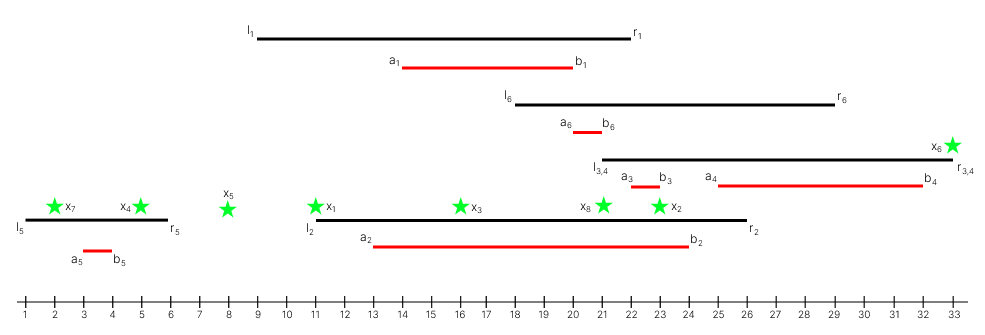
每个起始点的最优操作如下:
1. 先使用传送门 $1$,传送到区间 $[a_1, b_1] = [14, 20]$ 的点 $15$,再用传送门 $2$,传送到点 $21$,该点位于区间 $[l_4, r_4] = [21, 33]$,且在区间 $[a_2, b_2] = [13, 24]$ 内,然后传送到点 $b_4 = 32$。
2. 先使用传送门 $6$,传送到区间 $[a_6, b_6] = [20, 21]$ 的点 $20$,再用传送门 $2$,传送到点 $22$,该点同时在区间 $[l_4, r_4] = [21, 33]$ 和区间 $[a_2, b_2] = [13, 24]$ 内,然后传送到点 $b_4 = 32$。
3. 与第一个起始点操作相同。
4. 停留在 $x_4=5$,不使用任何传送门。
5. $8$ 不在任何区间内,Andrey 无法传送。
6. 停留在 $x_6=33$,不使用任何传送门。
7. 使用传送门 $5$,传送到点 $b_5 = 4$。
8. 与第一个起始点操作相同。
由 ChatGPT 4.1 翻译