CF185B Mushroom Scientists

众所周知，整个宇宙传统上使用三维笛卡尔坐标系。在该系统中，每个点对应三个实数坐标 $(x, y, z)$。在该坐标系下，宇宙中心到某点的距离通过以下公式计算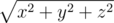：。为蘑菇大王工作的蘑菇科学家们认为，宇宙其实并不完全正确，宇宙中心到某点的距离应该是 $x^{a}·y^{b}·z^{c}$。 为了验证蘑菇科学家的度量，普通科学家给出了这样一个任务：找到 $x, y, z$ 满足 $0 \le x, y, z$ 且 $x + y + z \le S$，使得在蘑菇科学家的度量下，宇宙中心到点 $(x, y, z)$ 的距离最大。由于蘑菇科学家数学不好，这个任务就交给了你。 注意本题中认为 $0^{0}=1$。

第一行包含一个整数 $S$，$(1 \le S \le 10^{3})$——所求点坐标之和的最大值。 第二行包含三个用空格分隔的整数 $a, b, c$，$(0 \le a, b, c \le 10^{3})$——描述蘑菇科学家度量的参数。

输出三个实数，表示使蘑菇科学家度量下的距离最大化的点的坐标。若有多组解，输出任意一组满足限制的解即可。 宇宙中心到你所给出的点在蘑菇科学家度量下的距离的自然对数，与最大距离的自然对数不能相差超过 $10^{-6}$。我们认为 $ln(0)=-\infty$。

由 ChatGPT 5 翻译