CF1866C Completely Searching for Inversions

Pak Chanek has a directed acyclic graph (a directed graph that does not have any cycles) containing $ N $ vertices. Vertex $ i $ has $ S_i $ edges directed away from that vertex. The $ j $ -th edge of vertex $ i $ that is directed away from it, is directed towards vertex $ L_{i,j} $ and has an integer $ W_{i,j} $ ( $ 0\leq W_{i,j}\leq1 $ ). Another information about the graph is that the graph is shaped in such a way such that each vertex can be reached from vertex $ 1 $ via zero or more directed edges. Pak Chanek has an array $ Z $ that is initially empty. Pak Chanek defines the function dfs as follows: ```

```
// dfs from vertex i

void dfs(int i) {

    // iterate each edge of vertex i that is directed away from it

    for(int j = 1; j 
                            

The first line contains a single integer $ N $ ( $ 2 \leq N \leq 10^5 $ ) — the number of vertices in the graph. The following lines contain the description of each vertex from vertex $ 1 $ to vertex $ N $ . The first line of each vertex $ i $ contains a single integer $ S_i $ ( $ 0 \leq S_i \leq N-1 $ ) — the number of edges directed away from vertex $ i $ . The $ j $ -th of the next $ S_i $ lines of each vertex $ i $ contains two integers $ L_{i,j} $ and $ W_{i,j} $ ( $ 1 \leq L_{i,j} \leq N $ ; $ 0 \leq W_{i,j} \leq 1 $ ) — an edge directed away from vertex $ i $ that is directed towards vertex $ L_{i,j} $ and has an integer $ W_{i,j} $ . For each $ i $ , the values of $ L_{i,1} $ , $ L_{i,2} $ , ..., $ L_{i,S_i} $ are pairwise distinct. It is guaranteed that the sum of $ S_i $ over all vertices does not exceed $ 2 \cdot 10^5 $ . There are no cycles in the graph. Each vertex can be reached from vertex $ 1 $ via zero or more directed edges.

An integer representing the number of inversions in $ Z $ if Pak Chanek does dfs(1) once. Since the answer can be very big, output the answer modulo $ 998\,244\,353 $ .

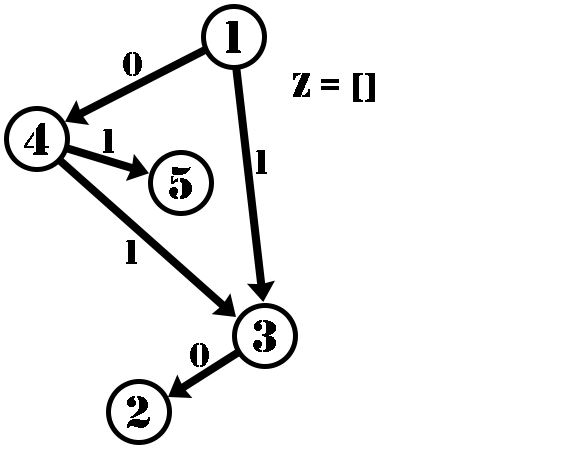
The following is the dfs(1) process on the graph.  In the end, $ Z=[0,1,0,1,1,0] $ . All of its inversions are $ (2,3) $ , $ (2,6) $ , $ (4,6) $ , and $ (5,6) $ .