CF1866I Imagination Castle

给定一个大小为 $N \times M$ 的棋盘（$N$ 行 $M$ 列）。每一行从上到下编号为 $1$ 到 $N$，每一列从左到右编号为 $1$ 到 $M$。第 $r$ 行第 $c$ 列的格子记作 $(r,c)$。棋盘上有 $K$ 个特殊格子，第 $i$ 个特殊格子为 $(X_i, Y_i)$。保证 $(1,1)$ 不是特殊格子。 现在有一种新发明的棋子，称为“城堡”。城堡的移动方式类似于国际象棋中的车，但有一点不同。在一次移动中，城堡只能沿同一行向右，或同一列向下移动。具体来说，若城堡当前在 $(r,c)$，则它可以移动到 $(r',c')$，当且仅当满足以下两个条件之一： - $r' = r$ 且 $c' > c$。 - $c' = c$ 且 $r' > r$。 Chaneka 和 Bhinneka 两人轮流进行游戏，Chaneka 先手。游戏开始时，城堡在 $(1,1)$。每一回合，当前玩家必须按照城堡的移动规则移动城堡。 如果某位玩家在她的回合将城堡移动到一个特殊格子，则该玩家获胜，游戏结束。如果在某一回合，城堡无法再移动，则当前玩家失败，游戏结束。 给定棋盘大小和所有特殊格子的位置，若两人都采取最优策略，判断最终胜者是谁。

第一行包含三个整数 $N$、$M$ 和 $K$（$1 \leq N, M \leq 2 \times 10^5$；$0 \leq K \leq \min(N \times M - 1, 2 \times 10^5)$），表示棋盘大小和特殊格子的数量。 接下来的 $K$ 行，每行包含两个整数 $X_i$ 和 $Y_i$（$1 \leq X_i \leq N$；$1 \leq Y_i \leq M$；$(X_i, Y_i) \neq (1,1)$），表示每个特殊格子的位置。所有特殊格子互不相同。

如果 Chaneka 获胜，输出 Chaneka；如果 Bhinneka 获胜，输出 Bhinneka。

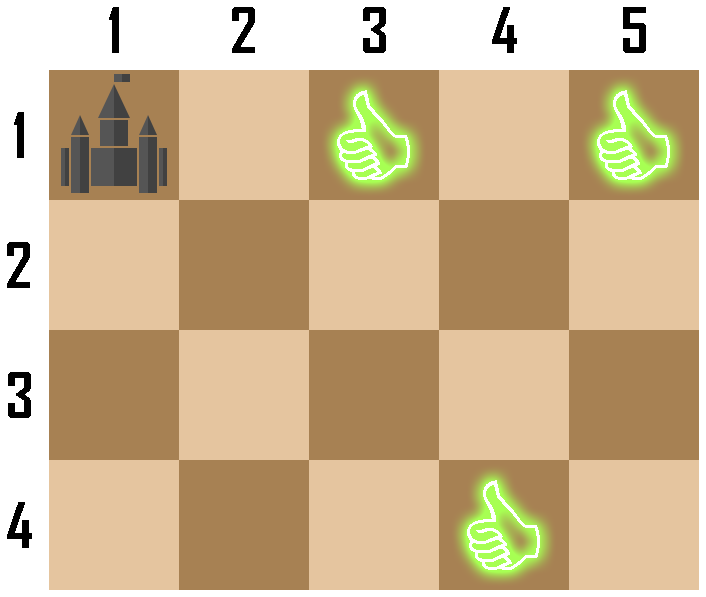
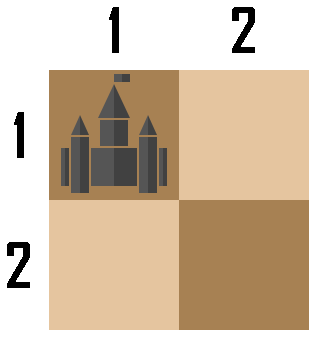
在第一个样例中，棋盘初始状态如下图所示。  Chaneka 可以在第一回合直接将城堡移动到特殊格子 $(1,3)$ 或 $(1,5)$，因此 Chaneka 获胜。 在第二个样例中，棋盘初始状态如下图所示。  Chaneka 只能将城堡移动到 $(1,2)$ 或 $(2,1)$。无论 Chaneka 如何选择，Bhinneka 都可以直接将城堡移动到 $(2,2)$。此后，Chaneka 无法再移动城堡，因此 Chaneka 失败，Bhinneka 获胜。 由 ChatGPT 4.1 翻译