CF1866K Keen Tree Calculation

There is a tree of $ N $ vertices and $ N-1 $ edges. The $ i $ -th edge connects vertices $ U_i $ and $ V_i $ and has a length of $ W_i $ . Chaneka, the owner of the tree, asks you $ Q $ times. For the $ j $ -th question, the following is the question format: - $ X_j $ $ K_j $ – If each edge that contains vertex $ X_j $ has its length multiplied by $ K_j $ , what is the diameter of the tree? Notes: - Each of Chaneka's question is independent, which means the changes in edge length do not influence the next questions. - The diameter of a tree is the maximum possible distance between two different vertices in the tree.

The first line contains a single integer $ N $ ( $ 2\leq N\leq10^5 $ ) — the number of vertices in the tree. The $ i $ -th of the next $ N-1 $ lines contains three integers $ U_i $ , $ V_i $ , and $ W_i $ ( $ 1 \leq U_i,V_i \leq N $ ; $ 1\leq W_i\leq10^9 $ ) — an edge that connects vertices $ U_i $ and $ V_i $ with a length of $ W_i $ . The edges form a tree. The $ (N+1) $ -th line contains a single integer $ Q $ ( $ 1\leq Q\leq10^5 $ ) — the number of questions. The $ j $ -th of the next $ Q $ lines contains two integers $ X_j $ and $ K_j $ as described ( $ 1 \leq X_j \leq N $ ; $ 1 \leq K_j \leq 10^9 $ ).

Output $ Q $ lines with an integer in each line. The integer in the $ j $ -th line represents the diameter of the tree on the $ j $ -th question.

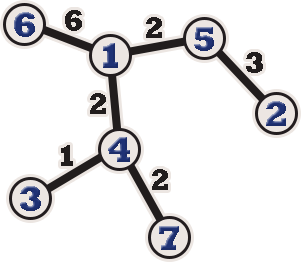
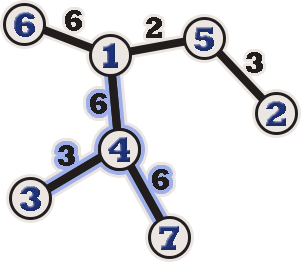
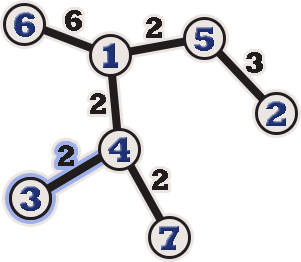
In the first example, the following is the tree without any changes.  The following is the tree on the $ 1 $ -st question.  The maximum distance is between vertices $ 6 $ and $ 7 $ , which is $ 6+6+6=18 $ , so the diameter is $ 18 $ . The following is the tree on the $ 2 $ -nd question.  The maximum distance is between vertices $ 2 $ and $ 6 $ , which is $ 3+2+6=11 $ , so the diameter is $ 11 $ .