CF1868C Travel Plan

中考结束后的暑假，Tom 和 Daniel 计划去旅行。 他们所在的国家有 $n$ 个城市，编号从 $1$ 到 $n$。这个国家的交通系统非常特殊。对于每个城市 $i$（$1 \le i \le n$），有如下规则： - 如果 $2i \le n$，则城市 $i$ 和城市 $2i$ 之间有一条道路； - 如果 $2i+1 \le n$，则城市 $i$ 和城市 $2i+1$ 之间有一条道路。 在制定旅行计划时，Daniel 会为每个城市选择一个 $1$ 到 $m$ 之间的整数值，对于第 $i$ 个城市我们记为 $a_i$。 设 $s_{i,j}$ 表示从城市 $i$ 到城市 $j$ 的简单路径 $^\dagger$ 上所有城市的最大值。一次旅行计划的得分为 $\sum_{i=1}^n\sum_{j=i}^n s_{i,j}$。 Tom 想知道所有可能的旅行计划的得分之和。Daniel 请你帮忙计算。你只需要输出答案对 $998\,244\,353$ 取模的结果即可。 $^\dagger$ 从城市 $x$ 到城市 $y$ 的简单路径是指一条连接它们且每个城市最多经过一次的路径。

输入的第一行包含一个整数 $t$（$1\le t\le 200$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例仅一行，包含两个整数 $n$ 和 $m$（$1\leq n\leq 10^{18}$，$1\leq m\leq 10^5$），分别表示城市数量和每个城市的最大值。 保证所有测试用例中 $m$ 的总和不超过 $10^5$。

对于每个测试用例，输出一个整数，表示所有可能旅行计划的得分之和，对 $998\,244\,353$ 取模。

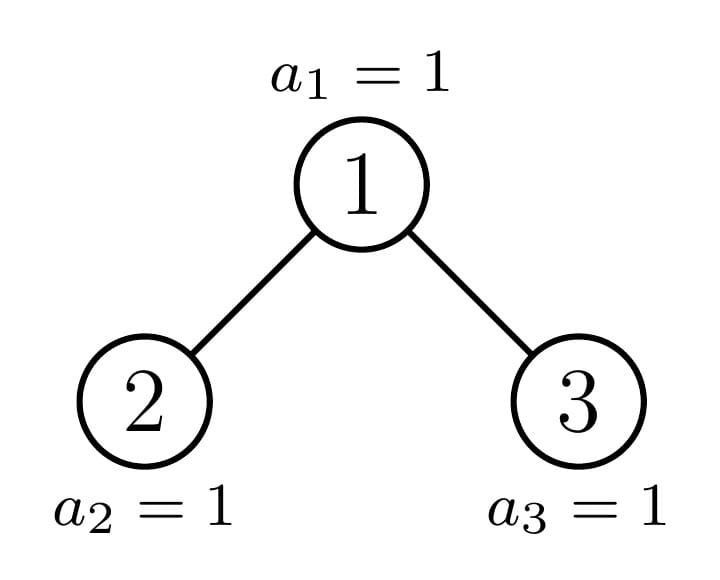
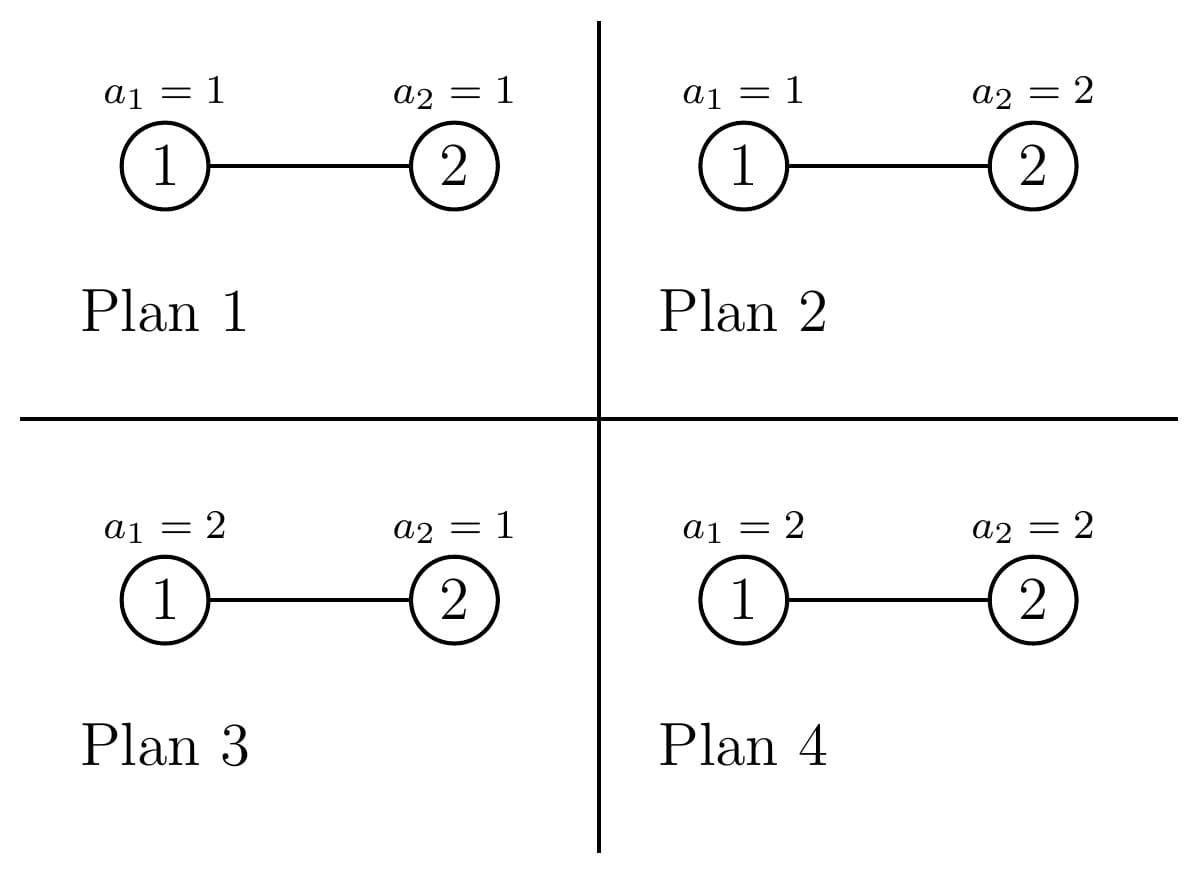
在第一个测试用例中，只有一种旅行计划：  路径 $1\rightarrow 1$：$s_{1,1}=a_1=1$。 路径 $1\rightarrow 2$：$s_{1,2}=\max(1,1)=1$。 路径 $1\rightarrow 3$：$s_{1,3}=\max(1,1)=1$。 路径 $2\rightarrow 2$：$s_{2,2}=a_2=1$。 路径 $2\rightarrow 1\rightarrow 3$：$s_{2,3}=\max(1,1,1)=1$。 路径 $3\rightarrow 3$：$s_{3,3}=a_3=1$。 得分为 $1+1+1+1+1+1=6$。 在第二个测试用例中，有四种可能的旅行计划：  计划 $1$ 的得分：$1+1+1=3$。 计划 $2$ 的得分：$1+2+2=5$。 计划 $3$ 的得分：$2+2+1=5$。 计划 $4$ 的得分：$2+2+2=6$。 因此，得分之和为 $3+5+5+6=19$。 由 ChatGPT 4.1 翻译