CF1868C Travel Plan

During the summer vacation after Zhongkao examination, Tom and Daniel are planning to go traveling. There are $ n $ cities in their country, numbered from $ 1 $ to $ n $ . And the traffic system in the country is very special. For each city $ i $ ( $ 1 \le i \le n $ ), there is - a road between city $ i $ and $ 2i $ , if $ 2i\le n $ ; - a road between city $ i $ and $ 2i+1 $ , if $ 2i+1\le n $ . Making a travel plan, Daniel chooses some integer value between $ 1 $ and $ m $ for each city, for the $ i $ -th city we denote it by $ a_i $ . Let $ s_{i,j} $ be the maximum value of cities in the simple $ ^\dagger $ path between cities $ i $ and $ j $ . The score of the travel plan is $ \sum_{i=1}^n\sum_{j=i}^n s_{i,j} $ . Tom wants to know the sum of scores of all possible travel plans. Daniel asks you to help him find it. You just need to tell him the answer modulo $ 998\,244\,353 $ . $ ^\dagger $ A simple path between cities $ x $ and $ y $ is a path between them that passes through each city at most once.

The first line of input contains a single integer $ t $ ( $ 1\le t\le 200 $ ) — the number of test cases. The description of test cases follows. The only line of each test case contains two integers $ n $ and $ m $ ( $ 1\leq n\leq 10^{18} $ , $ 1\leq m\leq 10^5 $ ) — the number of the cities and the maximum value of a city. It is guaranteed that the sum of $ m $ over all test cases does not exceed $ 10^5 $ .

For each test case output one integer — the sum of scores of all possible travel plans, modulo $ 998\,244\,353 $ .

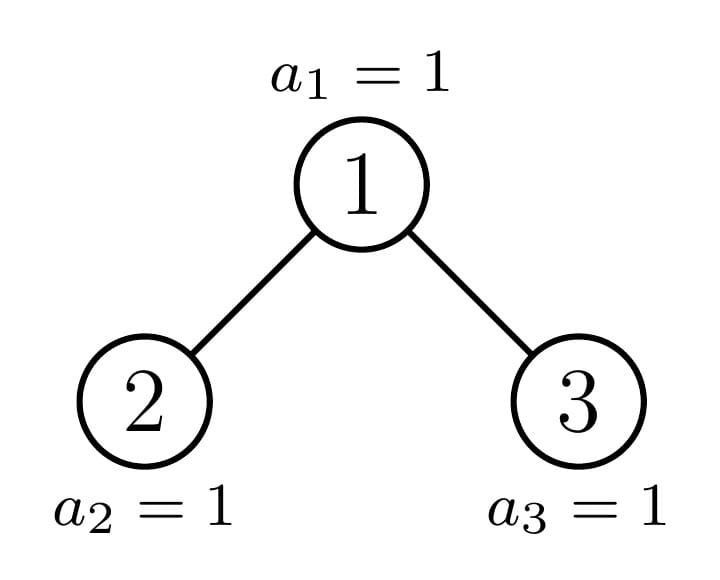In the first test case, there is only one possible travel plan: Path $ 1\rightarrow 1 $ : $ s_{1,1}=a_1=1 $ . Path $ 1\rightarrow 2 $ : $ s_{1,2}=\max(1,1)=1 $ . Path $ 1\rightarrow 3 $ : $ s_{1,3}=\max(1,1)=1 $ . Path $ 2\rightarrow 2 $ : $ s_{2,2}=a_2=1 $ . Path $ 2\rightarrow 1\rightarrow 3 $ : $ s_{2,3}=\max(1,1,1)=1 $ . Path $ 3\rightarrow 3 $ : $ s_{3,3}=a_3=1 $ . The score is $ 1+1+1+1+1+1=6 $ . 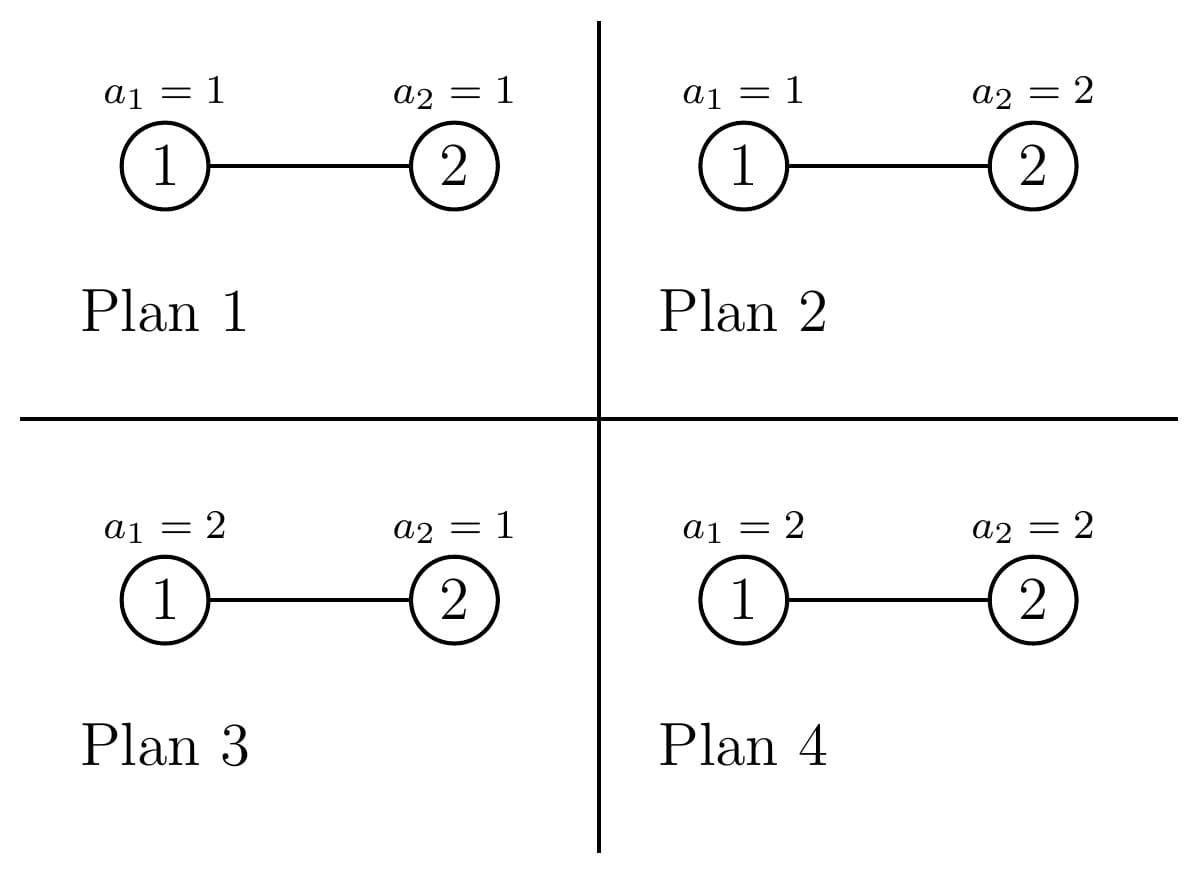In the second test case, there are four possible travel plans: Score of plan $ 1 $ : $ 1+1+1=3 $ . Score of plan $ 2 $ : $ 1+2+2=5 $ . Score of plan $ 3 $ : $ 2+2+1=5 $ . Score of plan $ 4 $ : $ 2+2+2=6 $ . Therefore, the sum of score is $ 3+5+5+6=19 $ .