CF1868D Flower-like Pseudotree

伪树是一种连通图，恰好包含一个环且没有自环。注意，伪树可以包含重边。可以证明，一个有 $n$ 个顶点的伪树总是包含 $n$ 条边。 在伪树中删除所有环上的边后，会形成一片森林 $^\dagger$。可以证明，森林中的每棵树都恰好包含一个在删除前属于环的顶点。如果当以环上的顶点作为根时，森林中所有树的深度 $^\ddagger$ 都相同，则称原伪树为“花状”。 你的朋友 sszcdjr 有一个包含 $n$ 个顶点和 $n$ 条边的花状伪树。但他忘记了伪树中的所有边。幸运的是，他还记得每个顶点的度数。具体来说，第 $i$ 个顶点的度数为 $d_i$。 你需要帮助 sszcdjr 构造一个可能的花状伪树，使得第 $i$ 个顶点的度数恰好为 $d_i$，或者告诉他这是不可能的。 $^\dagger$ 森林是指所有连通分量都是树的图。一个无环且无自环的连通图称为树。 $^\ddagger$ 一棵有根树的深度是指从根到该树中最远顶点的距离。

输入的第一行包含一个整数 $t$（$1\leq t\leq 10^5$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2\leq n\leq 10^6$），表示顶点数。 每个测试用例的第二行包含 $n$ 个整数 $d_1,d_2,\ldots,d_n$（$1\leq d_i\leq n$），表示每个顶点的度数。 保证所有测试用例中 $n$ 的总和不超过 $10^6$。

对于每个测试用例，如果存在一个可能的花状伪树： - 第一行输出 "Yes"（不区分大小写）。 - 接下来输出 $n$ 行，每行输出两个整数 $u_i$ 和 $v_i$，表示第 $i$ 条边连接的两个顶点。 如果不存在，输出一行 "No"（不区分大小写）。 你可以以任意大小写输出每个测试用例的第一行。例如，"yEs"、"yes"、"Yes" 和 "YES" 都会被识别为肯定回答。

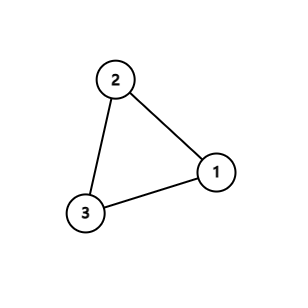
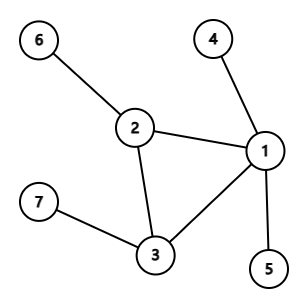
在第一个测试用例中，唯一可能的花状伪树为：  在伪树中删除所有环上的边后，每棵树的深度为 $0$。 在第二个测试用例中，可以证明不存在这样的花状伪树。 在第三个测试用例中，可能的花状伪树之一为：  由 ChatGPT 4.1 翻译