CF1869B 2D Traveling

Piggy 生活在一个带有笛卡尔坐标系的无限平面上。 平面上有 $n$ 个城市，编号从 $1$ 到 $n$，其中前 $k$ 个城市被定义为主要城市。第 $i$ 个城市的坐标为 $(x_i, y_i)$。 Piggy 作为一名经验丰富的旅行者，在中考结束后想要进行一次轻松的旅行。目前，他在城市 $a$，想要乘飞机前往城市 $b$。你可以在任意两个城市之间飞行，并且在旅行途中可以以任意顺序访问若干城市，但最终目的地必须是城市 $b$。 由于主要城市之间贸易活跃，主要城市之间可以免费乘坐飞机。具体来说，城市 $i$ 和城市 $j$ 之间的机票价格 $f(i, j)$ 定义如下： $$ f(i, j) = \begin{cases} 0, & \text{如果城市 } i \text{ 和城市 } j \text{ 都是主要城市} \\ |x_i - x_j| + |y_i - y_j|, & \text{否则} \end{cases} $$ Piggy 并不想节省时间，但他想节省金钱。因此，你需要告诉他，如果他可以乘坐任意次数的航班，所有机票的总费用的最小值是多少。

输入的第一行为一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行为四个整数 $n$、$k$、$a$ 和 $b$（$2 \le n \le 2 \cdot 10^5$，$0 \le k \le n$，$1 \le a, b \le n$，$a \ne b$），分别表示城市的数量、主要城市的数量、起点城市编号和终点城市编号。 接下来的 $n$ 行中，第 $i$ 行包含两个整数 $x_i$ 和 $y_i$（$-10^9 \le x_i, y_i \le 10^9$），表示第 $i$ 个城市的坐标。前 $k$ 行描述主要城市。保证所有城市的坐标两两不同。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示所有机票总费用的最小值。

在第一个测试用例中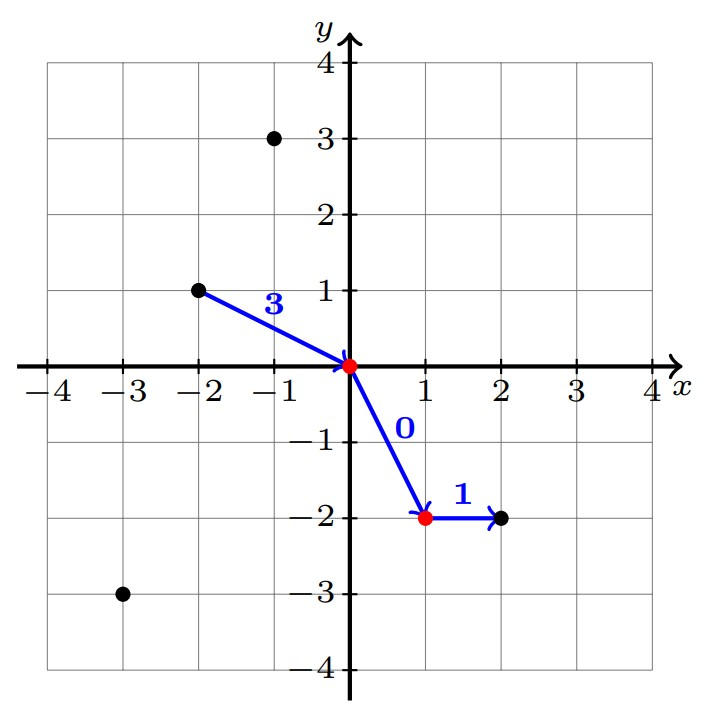：  主要城市用红色标记。最优的航班选择方式为：$3 \rightarrow 1 \rightarrow 2 \rightarrow 5$，总费用为 $3+0+1=4$。注意航班 $1 \rightarrow 2$ 的费用为 $0$，因为城市 $1$ 和 $2$ 都是主要城市。 在第二个测试用例中，只有 $2$ 个城市，唯一的方式是从城市 $1$ 飞到城市 $2$。 在第三个测试用例中，城市 $2$ 和 $4$ 都是主要城市，Piggy 可以直接从城市 $2$ 飞到城市 $4$，费用为 $0$。 在第四个测试用例中，Piggy 可以选择以下航班：$3 \rightarrow 2 \rightarrow 1$，总费用为 $11+11=22$。 由 ChatGPT 4.1 翻译