CF1873E Building an Aquarium

You love fish, that's why you have decided to build an aquarium. You have a piece of coral made of $ n $ columns, the $ i $ -th of which is $ a_i $ units tall. Afterwards, you will build a tank around the coral as follows: - Pick an integer $ h \geq 1 $ — the height of the tank. Build walls of height $ h $ on either side of the tank. - Then, fill the tank up with water so that the height of each column is $ h $ , unless the coral is taller than $ h $ ; then no water should be added to this column. For example, with $ a=[3,1,2,4,6,2,5] $ and a height of $ h=4 $ , you will end up using a total of $ w=8 $ units of water, as shown. 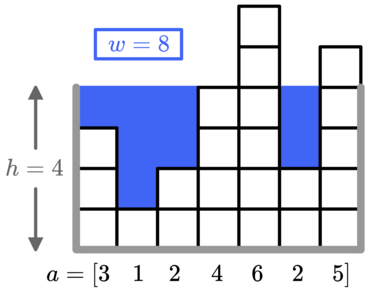 You can use at most $ x $ units of water to fill up the tank, but you want to build the biggest tank possible. What is the largest value of $ h $ you can select?

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The first line of each test case contains two positive integers $ n $ and $ x $ ( $ 1 \leq n \leq 2 \cdot 10^5 $ ; $ 1 \leq x \leq 10^9 $ ) — the number of columns of the coral and the maximum amount of water you can use. The second line of each test case contains $ n $ space-separated integers $ a_i $ ( $ 1 \leq a_i \leq 10^9 $ ) — the heights of the coral. The sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^5 $ .

For each test case, output a single positive integer $ h $ ( $ h \geq 1 $ ) — the maximum height the tank can have, so you need at most $ x $ units of water to fill up the tank. We have a proof that under these constraints, such a value of $ h $ always exists.

The first test case is pictured in the statement. With $ h=4 $ we need $ 8 $ units of water, but if $ h $ is increased to $ 5 $ we need $ 13 $ units of water, which is more than $ x=9 $ . So $ h=4 $ is optimal. In the second test case, we can pick $ h=4 $ and add $ 3 $ units to each column, using a total of $ 9 $ units of water. It can be shown that this is optimal. In the third test case, we can pick $ h=2 $ and use all of our water, so it is optimal.