CF1873H Mad City

Marcel 和 Valeriu 住在一座包含 $n$ 座建筑物和 $n$ 条无向边的城市。 初始时，Marcel 和 Valeriu 分别处于建筑物 $a$ 和建筑物 $b$。 Marcel 想要抓住 Valeriu。Valeriu 被 Marcel 抓住，当且仅当二人在某一时刻处于同一条边或同一座建筑物中。 在每次行动中，他们会选择移动到一个相邻的建筑物中，或停留在原地。由于 Valeriu 十分了解 Marcel，Valeriu 能够预测出 Marcel 的下一步行动。Valeriu 可以利用这些信息来制定行动路线。二人同时开始和结束行动。 对于任何两个建筑物，有且仅有一条路径将二者相连。 假设二人都绝顶聪明，判断 Valeriu 是否能够永远不被 Marcel 抓住。

**本题有多组测试数据。** 第一行包含一个整数 $t （1\le t\le 1000）$，代表测试数据的组数。 对于每组测试数据，第一行包含三个整数 $n，a，b（3\le n\le 2\times10^5，1\le a，b\le n）$，分别表示建筑物的数目、Marcel 与 Valeriu 的初始位置。 接下来的 $n$ 行，每行包含两个整数 $u_i，v_i（1 \le u_i，v_i\le n）$，表示存在一条连接建筑物 $u$ 和 $v$ 的无向边。数据保证不存在自环或重边。 所有测试数据中的 $n$ 之和不超过 $2\times 10^5$。 数据保证图是联通的。

对于每组测试数据，如果 Marce 永远无法追上 Valeriu，在单独的一行中输出 `YES`，否则输出 `NO`（输出不区分字母的大小写，例如假设某组测试数据中 Marce 永远无法追上 Valeriu，输出 `Yes`，`yes` 或 `YeS` 都被视为正确答案）。

In the first test case the graph looks as follows: 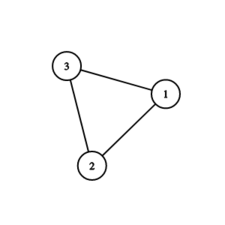 Marcel starts at building $ 2 $ , while Valeriu starts at building $ 1 $ . Valeriu knows which way Marcel will move around the triangle, and he can simply always move in the same way to avoid Marcel forever.In the second test case the graph looks as follows: 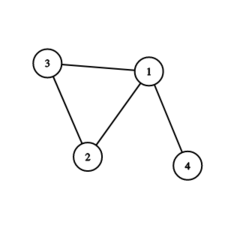 Marcel starts at building $ 1 $ , while Valeriu starts at building $ 4 $ . Marcel can go to building $ 4 $ on his first move and win, since Valeriu must either go to building $ 1 $ (then he meets Marcel on the road from $ 1 $ to $ 4 $ ) or stay at building $ 4 $ (then he meets Marcel at building $ 4 $ ). So there is no strategy for Valeriu to win.