CF1876E Ball-Stackable

看到这个题目标题，你就知道这绝对不会是一个图论题。 Chaneka 有一个包含 $n$ 个顶点和 $n-1$ 条边的图。有些边是有向的，有些边是无向的。第 $i$ 条边连接顶点 $u_i$ 和顶点 $v_i$。如果 $t_i=0$，则第 $i$ 条边是无向边；如果 $t_i=1$，则第 $i$ 条边是从 $u_i$ 指向 $v_i$ 的有向边。已知如果将所有边都视为无向边，这个图会变成一棵树 $^\dagger$。 Chaneka 想要为所有无向边定向，并给每条边染色（不同的边可以有相同的颜色）。 在完成上述操作后，假设 Chaneka 从任意顶点 $x$ 出发，走到任意顶点 $y$（可能 $x=y$），沿途经过一条或多条边。她可以顺着边的方向或逆着边的方向走每一条边，也可以多次经过同一个顶点或边。在行走过程中，Chaneka 维护一个最初为空的球堆栈。每当她经过一条边时，执行如下操作： - 如果 Chaneka 按边的正方向经过，则在栈顶放入一个与该边颜色相同的新球。 - 如果 Chaneka 逆着边的方向经过，则从栈顶取出一个球。 如果每次逆向经过边时栈都不为空，则称该路径为“可堆栈路径”。 如果一条路径是可堆栈路径，并且每次逆向经过边时取出的球颜色与该边颜色相同，则称该路径为“球可堆栈路径”。 请判断是否可以为所有无向边定向并给每条边染色，使得所有可堆栈路径都是球可堆栈路径。如果可以，请给出一种构造方案，使得使用的不同颜色数目在所有合法方案中最大。如果有多种方案，输出任意一种。 $^\dagger$ 一棵树是一个连通且无环的图。

第一行包含一个整数 $n$（$2\leq n\leq 10^5$），表示图中顶点的数量。 接下来的 $n-1$ 行中，第 $i$ 行包含三个整数 $u_i$、$v_i$ 和 $t_i$（$1\leq u_i,v_i\leq n$；$0\leq t_i\leq 1$），表示一条连接顶点 $u_i$ 和 $v_i$ 的边。如果 $t_i=0$，则为无向边；如果 $t_i=1$，则为从 $u_i$ 指向 $v_i$ 的有向边。将所有边视为无向边后，图为一棵树。

如果无解，输出一行 $-1$。 否则，输出 $n$ 行描述你的构造方案。第一行包含一个整数 $z$，表示使用的不同颜色的数量。接下来的 $n-1$ 行中，第 $i$ 行包含三个整数 $p$、$q$ 和 $c$（$1\leq p,q\leq n$；$1\leq c\leq z$），表示第 $i$ 条边从 $p$ 指向 $q$，颜色为 $c$。如果有多种方案，输出任意一种。 注意，因为你需要使用 $z$ 种不同的颜色，所以每种颜色 $1$ 到 $z$ 必须至少出现一次。

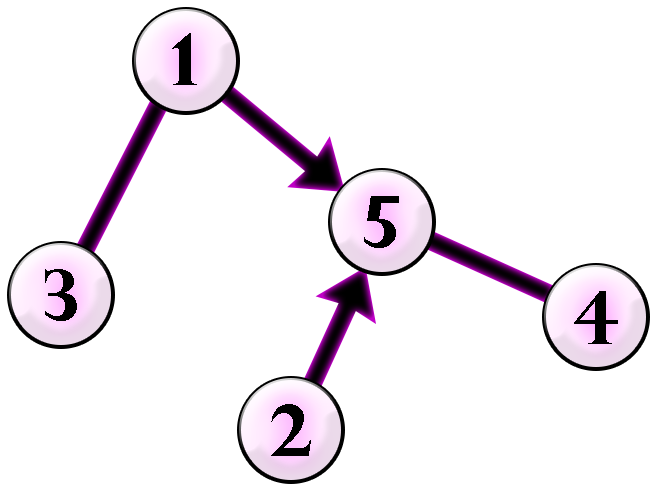
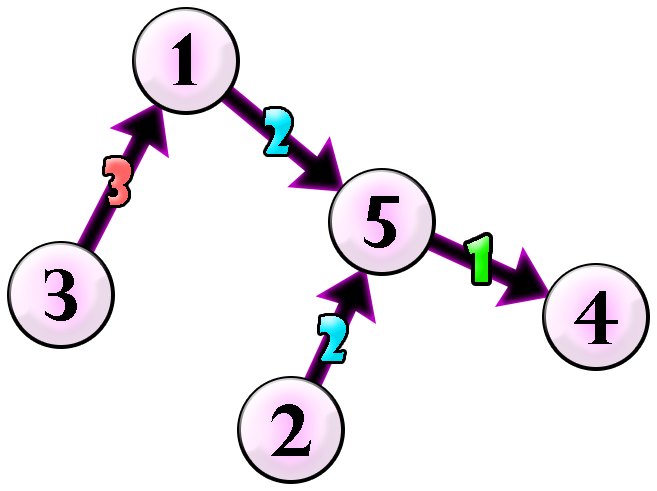
下图为给定的图。  Chaneka 可以将所有无向边定向并染色如下。  例如，考虑一条可堆栈路径 $3→1→5→2→5→4→5$。我们来验证这条路径是球可堆栈路径。 1. Chaneka 从顶点 $3$ 出发，栈为 $[]$。 2. Chaneka 走到顶点 $1$，放入颜色为 $3$ 的球，栈为 $[3]$。 3. Chaneka 走到顶点 $5$，放入颜色为 $2$ 的球，栈为 $[3,2]$。 4. Chaneka 走到顶点 $2$，取出颜色为 $2$ 的球（与边颜色相同），栈为 $[3]$。 5. Chaneka 走到顶点 $5$，放入颜色为 $2$ 的球，栈为 $[3,2]$。 6. Chaneka 走到顶点 $4$，放入颜色为 $1$ 的球，栈为 $[3,2,1]$。 7. Chaneka 走到顶点 $5$，取出颜色为 $1$ 的球（与边颜色相同），栈为 $[3,2]$。 由于每次取出的球颜色都与经过的边颜色相同，因此上述路径是球可堆栈路径。可以证明，如果按照上图所示的方式定向和染色所有边，则任意可堆栈路径都是球可堆栈路径。 由 ChatGPT 4.1 翻译