CF1878G wxhtzdy ORO Tree

在（终于）获得 IOI 2023 资格后，wxhtzdy 非常高兴，于是他决定做大多数竞赛程序员都会做的事情：试图猜测 IOI 上会出现哪些题目。在这个过程中，他意外地出了一道题，他觉得这题非常酷。 给定一棵有 $n$ 个顶点和 $n-1$ 条边的树（连通无环图）。第 $i$ 个顶点（$1 \le i \le n$）有一个权值 $a_i$。 我们定义 $g(u, v)$ 为从 $u$ 到 $v$ 的最短路径上所有顶点的权值的按位或。例如，假设我们要计算 $g(3, 4)$，以样例中第一组数据的树为例。从 $3$ 到 $4$ 的路径经过顶点 $3$、$1$、$4$，那么 $g(3, 4) = a_3 \mid a_1 \mid a_4$（这里 $\mid$ 表示按位或运算）。 此外，给定 $q$ 个询问，每个询问如下： 给定 $x$ 和 $y$。我们考虑所有在从 $x$ 到 $y$ 的最短路径上的顶点 $z$（包括 $x$ 和 $y$）。 定义顶点 $z$ 的“美丽度”为 $g(x, z)$ 的非零二进制位数与 $g(y, z)$ 的非零二进制位数之和。你需要求出从 $x$ 到 $y$ 的最短路径上所有顶点 $z$ 的最大美丽度。 由于他在 SIO 上做了一道只输出的题目后脑子已经很累（他必须做这题才能获得 IOI 资格），所以他希望你能帮他解决这个问题。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$）——表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 2 \times 10^5$）——表示顶点数。 每个测试用例的第二行包含 $n$ 个正整数 $a_1, a_2, \dots, a_n$（$1 \le a_v \le 10^9$）——表示每个顶点的权值，第 $i$ 个数对应第 $i$ 个顶点。 接下来的 $n-1$ 行描述树的结构。 每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n, u \ne v$），表示顶点 $u$ 和 $v$ 之间有一条边。 接下来一行包含一个整数 $q$（$1 \le q \le 10^5$）——表示询问的数量。 接下来的 $q$ 行，每行包含两个整数 $x, y$（$1 \le x, y \le n$），表示每个询问的两个顶点。 保证所有测试用例中 $n$ 的总和不超过 $2 \times 10^5$。 保证所有测试用例中 $q$ 的总和不超过 $10^5$。

对于每个测试用例，输出 $q$ 个整数，每个整数为对应询问的答案。

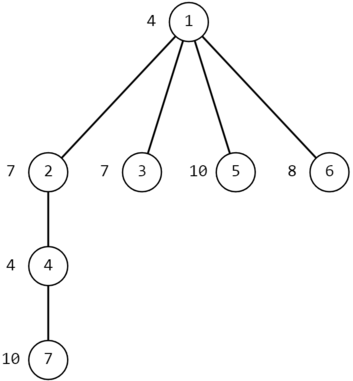
下图展示了第二个样例中第一组测试数据的树结构。  在第一个询问中，$x=7$，$y=5$。从 $7$ 到 $5$ 的最短路径为 $7-4-2-1-5$。 我们来计算该路径上顶点 $7$ 的美丽度。$g(7,7)=a_7=10=(1010)_2$，$g(5,7)=a_5 \mid a_1 \mid a_2 \mid a_4 \mid a_7=10 \mid 4 \mid 7 \mid 4 \mid 10=15=(1111)_2$，所以美丽度为 $2+4=6$。 再计算顶点 $4$ 的美丽度。$g(7,4)=a_7 \mid a_4=10 \mid 4=14=(1110)_2$，$g(5,4)=a_5 \mid a_1 \mid a_2 \mid a_4=10 \mid 4 \mid 7 \mid 4=15=(1111)_2$，美丽度为 $3+4=7$。 再计算顶点 $2$ 的美丽度。$g(7,2)=a_7 \mid a_4 \mid a_2=10 \mid 4 \mid 7=15=(1111)_2$，$g(5,2)=a_5 \mid a_1 \mid a_2=10 \mid 4 \mid 7=15=(1111)_2$，美丽度为 $4+4=8$。 再计算顶点 $1$ 的美丽度。$g(7,1)=a_7 \mid a_4 \mid a_2 \mid a_1=10 \mid 4 \mid 7 \mid 4=15=(1111)_2$，$g(5,1)=a_5 \mid a_1=10 \mid 4=14=(1110)_2$，美丽度为 $4+3=7$。 最后计算顶点 $5$ 的美丽度。$g(7,5)=a_7 \mid a_4 \mid a_2 \mid a_1 \mid a_5=10 \mid 4 \mid 7 \mid 4 \mid 10=15=(1111)_2$，$g(5,5)=a_5=10=(1010)_2$，美丽度为 $4+2=6$。 该路径上的最大美丽度出现在顶点 $2$，为 $8$。 由 ChatGPT 4.1 翻译