CF1879B Chips on the Board

You are given a board of size $ n \times n $ ( $ n $ rows and $ n $ colums) and two arrays of positive integers $ a $ and $ b $ of size $ n $ . Your task is to place the chips on this board so that the following condition is satisfied for every cell $ (i, j) $ : - there exists at least one chip in the same column or in the same row as the cell $ (i, j) $ . I. e. there exists a cell $ (x, y) $ such that there is a chip in that cell, and either $ x = i $ or $ y = j $ (or both). The cost of putting a chip in the cell $ (i, j) $ is equal to $ a_i + b_j $ . For example, for $ n=3 $ , $ a=[1, 4, 1] $ and $ b=[3, 2, 2] $ . One of the possible chip placements is as follows: 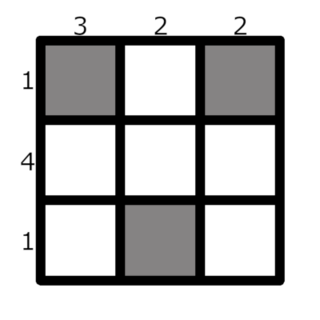 White squares are emptyThe total cost of that placement is $ (1+3) + (1+2) + (1+2) = 10 $ . Calculate the minimum possible total cost of putting chips according to the rules above.

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 3 \cdot 10^5 $ ). The second line contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \le a_i \le 10^9 $ ). The third line contains $ n $ integers $ b_1, b_2, \dots, b_n $ ( $ 1 \le b_i \le 10^9 $ ). The sum of $ n $ over all test cases doesn't exceed $ 3 \cdot 10^5 $ .

For each test case, print a single integer — the minimum possible total cost of putting chips according to the rules.

The first test case of the example is described in the statement.