CF1879B Chips on the Board

给定一个大小为 $n \times n$ 的棋盘（$n$ 行 $n$ 列），以及两个长度为 $n$ 的正整数数组 $a$ 和 $b$。 你的任务是在棋盘上放置筹码，使得对于每一个格子 $(i, j)$，都满足以下条件： - 在与该格子 $(i, j)$ 同一行或同一列的某个格子中，至少有一个筹码。也就是说，存在一个格子 $(x, y)$，该格子上有筹码，并且 $x = i$ 或 $y = j$（或两者都成立）。 在格子 $(i, j)$ 放置一个筹码的代价为 $a_i + b_j$。 例如，当 $n=3$，$a=[1, 4, 1]$，$b=[3, 2, 2]$ 时，一种可能的放置方式如下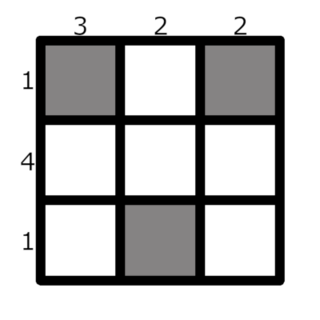：  白色格子为空。 该放置方式的总代价为 $(1+3) + (1+2) + (1+2) = 10$。 请计算在满足上述规则的前提下，放置筹码的最小总代价。

第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 3 \cdot 10^5$）。 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$（$1 \le a_i \le 10^9$）。 第三行包含 $n$ 个整数 $b_1, b_2, \dots, b_n$（$1 \le b_i \le 10^9$）。 所有测试用例中 $n$ 的总和不超过 $3 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示在满足条件的情况下放置筹码的最小总代价。

样例的第一个测试用例已在题目描述中给出。 由 ChatGPT 4.1 翻译