CF1881C Perfect Square
题目描述
Kristina有一个大小为$n \times n$的矩阵,里面填满了小写拉丁字母。$n$的值是偶数。
她想要改变一些字符,使得她的矩阵变成一个完美方阵。一个矩阵被称为完美方阵,如果它在顺时针旋转90度后仍然保持不变。
这是一个顺时针旋转矩阵90度的例子:
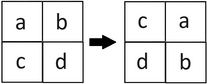
在一次操作中,Kristina可以选择任意一个单元格,并将其值替换为字母表中的下一个字符。如果字符等于"z",则它的值不会改变。
找出使得矩阵成为完美方阵所需的最小操作次数。
例如,如果$4 \times 4$的矩阵如下所示:
$ \begin{matrix} a & b & b & a \\ b & c & \textbf{b} & b \\ b & c & c & b\\ a & b & b & a \\ \end{matrix} $
那么只需要对加粗的字母b进行1次操作即可。
输入格式
输入的第一行包含一个整数$t$($1 \le t \le 10^2$)——测试用例的数量。
然后是每个测试用例的描述。
每个测试用例的第一行包含一个偶数$n$($2 \le n \le 10^3$)——矩阵的行数和列数。
接下来是$n$行,每行包含$n$个小写拉丁字母。
保证所有测试用例中$n$的总和不超过$10^3$。
输出格式
对于每个测试用例,输出一个单独的数字,表示Kristina获得完美方阵所需的最小操作次数。
## 样例 #1
### 样例输入 #1
```
5
4
abba
bcbb
bccb
abba
2
ab
ba
6
codefo
rcesco
deforc
escode
forces
codefo
4
baaa
abba
baba
baab
4
bbaa
abba
aaba
abba
```
### 样例输出 #1
```
1
2
181
5
9
```
说明/提示
第一个测试用例在问题描述中已经解释过了。