CF1881F Minimum Maximum Distance

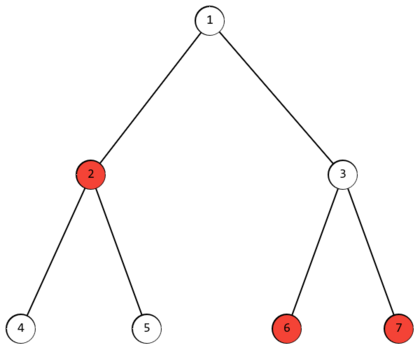You have a tree with $ n $ vertices, some of which are marked. A tree is a connected undirected graph without cycles. Let $ f_i $ denote the maximum distance from vertex $ i $ to any of the marked vertices. Your task is to find the minimum value of $ f_i $ among all vertices. For example, in the tree shown in the example, vertices $ 2 $ , $ 6 $ , and $ 7 $ are marked. Then the array $ f(i) = [2, 3, 2, 4, 4, 3, 3] $ . The minimum $ f_i $ is for vertices $ 1 $ and $ 3 $ .

The first line contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains two integers $ n $ and $ k $ ( $ 1 \le k \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree and the number of marked vertices, respectively. The second line of each test case contains $ k $ integers $ a_i $ ( $ 1 \le a_i \le n, a_{i-1} < a_i $ ) — the indices of the marked vertices. The next $ n - 1 $ lines contain two integers $ u_i $ and $ v_i $ — the indices of vertices connected by the $ i $ -th edge. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output a single integer — the minimum value of $ f_i $ among all vertices.