CF1881F Minimum Maximum Distance

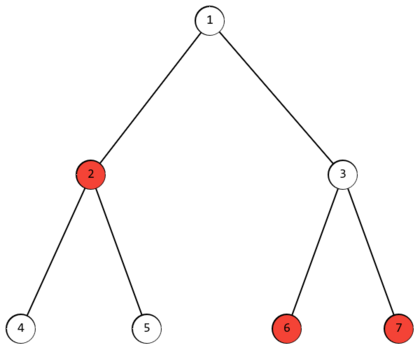
一棵树有 $n$ 个点，其中有一些节点被打了标记。保证树是联通且无环的。 定义 $ f_i $ 为第 $ i $ 个节点到所有被标记节点距离的最大值。 你的任务是找出所有点的 $ f_i $ 的最小值。  举个例子，一棵树如上图所示，被标记节点为 $ 2 $ , $ 6 $ , $ 7 $。 因此 $ f(i) = [2, 3, 2, 4, 4, 3, 3] $。$ f_i $ 最小的为 $ 1 $ 和 $ 3 $ 节点，且最小值为 $2$。

第一行包含一个整数 $ t $ ( $ 1 \le t \le 10^4 $ ) — 表示 $t$ 组测试数据。 每组测试数据，第一行包含两个整数，$ n $ 和 $ k $ ( $ 1 \le k \le n \le 2 \times 10^5 $ ) — 表示树的节点个数和被标记节点的个数。 每组数据第二行包含 $ k $ 整数 $ a_i $ ( $ 1 \le a_i \le n, a_{i-1} < a_i $ ) — 表示被标记节点的节点编号。 接下来 $ n - 1 $ 行，包含两个整数 $ u_i , v_i $ — 表示 $u_i$ 与 $v_i$ 之间有一条边。 数据保证所有测试数据 $ n $ 之和不超过 $ 2 \times 10^5 $。

对于每组数据，输出一行，包含一个整数 — 代表所有点的 $ f_i $ 中的最小值。