CF1885A Deterministic Scheduling for Extended Reality over 5G and Beyond

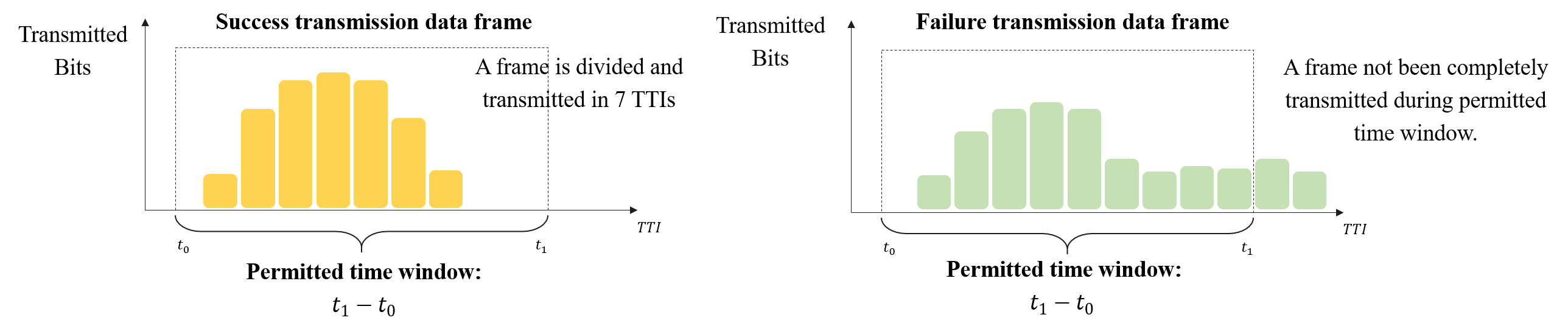
### 背景 扩展现实（XR）服务是未来通信中的一项非常有潜力的应用。在无线通信中，XR 数据通过无线电在基站和移动终端之间传输。一个区域通常被划分为多个小区，每个小区内有一个基站来服务用户。每个基站通常可以同时服务许多用户，而同一用户也可能由多个基站同时服务。 ### 任务 这次竞赛的任务是为 XR 服务设计一个调度算法。通过合理分配无线电资源，我们希望能够最大化成功传输的 XR 数据帧数。如下图所示：如果数据帧在规定的传输时间窗口内未能完整传输，则视为传输失败。  因此，可以将该任务的目标建模为： $$ \mathcal{P}: \max \sum_j f_j \tag{1} $$ 这里，$ f_j $ 表示第 $ j $ 帧的传输结果：当实际传输的比特数 $ g_j $ （通过公式 (5) 计算）不小于帧的大小 $ TBS_j $ 时， $ f_j $ 则为1，表示成功传输，否则为0。 为了优化用户体验，需要设计一种调度算法来高效分配有限的无线电资源： - **时域资源**：划分为若干个传输时间间隔（TTI），每个 TTI 的传输时间是 $ 0.5 $ 毫秒。 - **频域资源**：划分为若干个资源块组（RBG），每个 RBG 的传输带宽是 $ 5760 $ kHz。 - **功率域资源**：每个小区设定了一个固定的最大发射功率来服务用户。 总的来说，引入了两个优化变量来表示调度结果： - $ b_{rnt}^{(k)} $ 是表示资源是否分配给用户的布尔变量。 - $ p_{rnt}^{(k)} $ 是一个非负连续变量，表示在 TTI $ t $ 时分配给用户 $ n $ 的功率，要满足每个 RBG 的功率不能超过 4，且所有 RBG 的总功率不能超过 $ R $。 分配好无线电资源后，就可以为用户提供 XR 数据传输。假设第 $ j $ 帧属于第 $ n $ 个用户，那么该帧的实际传输比特数 $ g_j $ 可由以下公式给出： $$ g_j = W \times \sum_{t=t_{0,j}}^{t_{1,j}} \sum_k \sum_r b_{r n t}^{(k)} \times \log_2(1 + s_{n t}^{(k)}). \tag{5} $$ 其中，$ W \times \log_2(1 + s_{nt}^{(k)}) $ 是传输的数据量，根据香农公式计算，$ s_{nt}^{(k)} $ 为用户 $ n $ 在小区 $ k $ 的 TTI $ t $ 时的信号与干扰加噪声比，$ W=192 $ 是一个资源块组中的可用频率资源元素的常量值。$ t_{0,j} $ 和 $ t_{1,j} $ 分别是第 $ j $ 帧的开始和结束 TTI。 最终，给出 SINR 的公式： $$ s_{nt}^{(k)} = \left( \prod_{r, b_{rnt}^{(k)} = 1} s_{rnt}^{(k)} \right)^{\frac{1}{\sum_r b_{rnt}^{(k)}}} \tag{6} $$ $$ s_{rnt}^{(k)} = \frac{s_{0, rnt}^{(k)} \times p_{rnt}^{(k)} \times \prod_{m \neq n} e^{d_{mrn}^{(k)} \times b_{rmt}^{(k)}}}{1 + \sum_{k' \neq k, n' \neq n} s_{0, rnt}^{(k')} \times p_{rn't}^{(k')} \times e^{-d_{n'rn}^{(k')}}} \tag{7} $$ 公式 (6) 描述了用户级别有效 SINR 的计算：这是所有分配 RBG SINR 的几何平均值。公式 (7) 则描述了 RBG 级别有效 SINR 的计算。$ s_{0, rnt}^{(k)} $ 是 RBG 初始信噪比，$ d_{mrn}^{(k)} $ 是用户间的干扰因子，二者均为给定常量。请注意，当多个用户共享同一资源时，SINR 将会下降。 总之，参赛者需要找到一个高效的资源分配方案，使得更多 XR 数据帧可以被成功传输。

单个测试用例的输入包含 $ (4 + R \cdot K \cdot T + N \cdot R \cdot K + 1 + J) $ 行，包括用户数、基站数、TTI 数、RBG 数、初始信噪比、干扰因子、帧数及帧信息。 具体内容如下： - 第 1 行：用户数 $ N $，整数，范围 $ 1 \leq N \leq 100 $，用户编号为 $ 0 $ 至 $ N-1 $。 - 第 2 行：小区数 $ K $，整数，范围 $ 1 \leq K \leq 10 $，小区编号为 $ 0 $ 至 $ K-1 $。 - 第 3 行：TTI 数 $ T $，整数，范围 $ 1 \leq T \leq 1000 $，TTI 编号为 $ 0 $ 至 $ T-1 $。 - 第 4 行：RBG 数 $ R $，整数，范围 $ 1 \leq R \leq 10 $，RBG 编号为 $ 0 $ 至 $ R-1 $。 - 第 5 行至第 $ (4+R \cdot K \cdot T) $ 行：初始信噪比 $ s_{0, rnt}^{(k)} $，浮点数，范围 $ 0 < s_{0, rnt}^{(k)} < 10,000 $，每行有 $ N $ 个元素，对应 $ N $ 个用户。 - 第 $ (5+R \cdot K \cdot T) $ 行至第 $ (4+R \cdot K \cdot T + N \cdot R \cdot K) $ 行：干扰因子 $ d_{mrn}^{(k)} $，浮点数，范围 $ -2 \leq d_{mrn}^{(k)} \leq 0 $。 - 第 $ (5+R \cdot K \cdot T + N \cdot R \cdot K) $ 行：帧数 $ J $，整数，范围 $ 1 \leq J \leq 5000 $。 - 接下来的 $ J $ 行：每行包含 5 个整数，分别代表：帧 ID，大小 $ TBS_j $（范围 $ 0 < TBS_j \leq 100,000 $），所属用户 ID，初始 TTI $ t_{0,j} $ 和连续传输的 TTI 数量 $ t_{d,j} $。 确保每个用户在每个 TTI 上最多拥有一个帧。

每个输入用例的输出是 $ p_{rnt}^{(k)} $ 的优化结果。共 $ R \cdot K \cdot T $ 行，每行 $ N $ 个元素，表示相应用户的功率变量，确保 $ p_{rnt}^{(k)} > 0 $ 表示 $ b_{rnt}^{(k)}=1 $。 若输出不符合（4）要求，将被判定为错误答案并得分为 0。在时间窗口之外的传输虽然有效，但可能导致资源浪费，从而降低得分。 ### 评分 优化目标是尽量多地成功调度帧数。在帧数相同的情况下，比较功率使用度。评分公式为 $ Score = X - 10^{-6} \times p $，其中 $ X $ 为成功调度的帧数，$ p $ 为总功率使用量。 提交的总分是各测试用例的得分累加。 **本翻译由 AI 自动生成**

Two sets of tests are prepared in this problem. For the duration of the competition, each submission is tested on the preliminary set of tests. When the competition is finished, for each contestant: The jury takes the latest submission with non-zero score on preliminary tests; This submission is tested on the final set of tests for the final rank; The two sets of tests are generated from the same pool of data, based on the real word data.