CF1886B Fear of the Dark

Monocarp tries to get home from work. He is currently at the point $ O = (0, 0) $ of a two-dimensional plane; his house is at the point $ P = (P_x, P_y) $ . Unfortunately, it is late in the evening, so it is very dark. Monocarp is afraid of the darkness. He would like to go home along a path illuminated by something. Thankfully, there are two lanterns, located in the points $ A = (A_x, A_y) $ and $ B = (B_x, B_y) $ . You can choose any non-negative number $ w $ and set the power of both lanterns to $ w $ . If a lantern's power is set to $ w $ , it illuminates a circle of radius $ w $ centered at the lantern location (including the borders of the circle). You have to choose the minimum non-negative value $ w $ for the power of the lanterns in such a way that there is a path from the point $ O $ to the point $ P $ which is completely illuminated. You may assume that the lanterns don't interfere with Monocarp's movement. 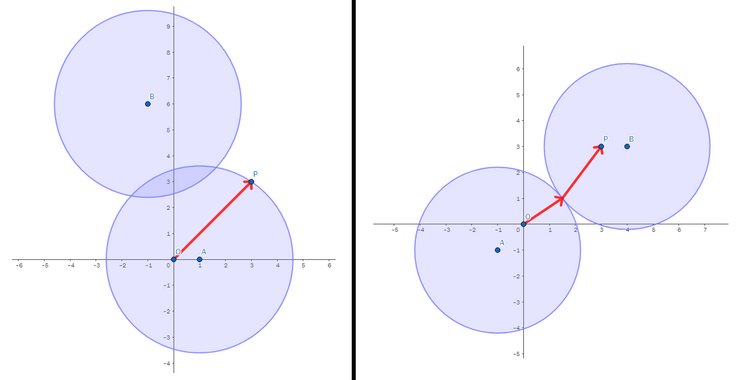 The picture for the first two test cases

The first line of the input contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Each test case consists of three lines: - the first line contains two integers $ P_x $ and $ P_y $ ( $ -10^3 \le P_x, P_y \le 10^3 $ ) — the location of Monocarp's house; - the second line contains two integers $ A_x $ and $ A_y $ ( $ -10^3 \le A_x, A_y \le 10^3 $ ) — the location of the first lantern; - the third line contains two integers $ B_x $ and $ B_y $ ( $ -10^3 \le B_x, B_y \le 10^3 $ ) — the location of the second lantern. Additional constraint on the input: - in each test case, the points $ O $ , $ P $ , $ A $ and $ B $ are different from each other.

For each test case, print the answer on a separate line — one real number equal to the minimum value of $ w $ such that there is a completely illuminated path from the point $ O $ to the point $ P $ . Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ — formally, if your answer is $ a $ , and the jury's answer is $ b $ , your answer will be accepted if $ \dfrac{|a - b|}{\max(1, b)} \le 10^{-6} $ .