CF1886B Fear of the Dark

Monocarp 想要从公司回家。他现在位于二维平面上的点 $O = (0, 0)$，他的家在点 $P = (P_x, P_y)$。 不幸的是，现在已经很晚了，天很黑。Monocarp 害怕黑暗。他希望沿着被照亮的路径回家。 幸运的是，有两个灯笼，分别位于点 $A = (A_x, A_y)$ 和 $B = (B_x, B_y)$。你可以选择任意非负数 $w$，并将两个灯笼的亮度都设置为 $w$。如果一个灯笼的亮度为 $w$，它会照亮以该灯笼为圆心、半径为 $w$ 的圆（包括圆的边界）。 你需要选择最小的非负亮度 $w$，使得存在一条从点 $O$ 到点 $P$ 的路径，且这条路径完全被照亮。你可以假设灯笼不会影响 Monocarp 的移动。 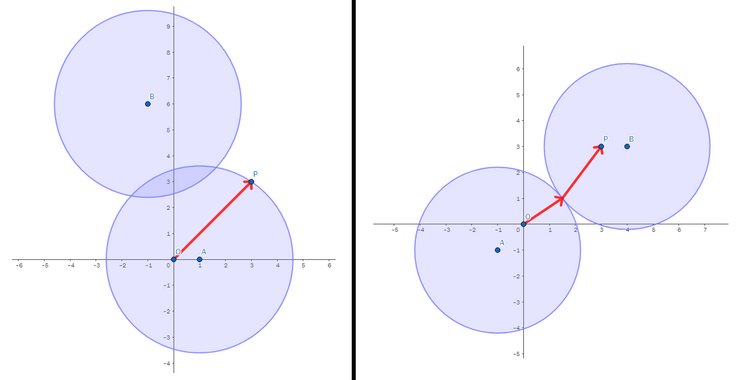 前两个测试用例的示意图

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例包含三行： - 第一行包含两个整数 $P_x$ 和 $P_y$（$-10^3 \le P_x, P_y \le 10^3$），表示 Monocarp 家的位置； - 第二行包含两个整数 $A_x$ 和 $A_y$（$-10^3 \le A_x, A_y \le 10^3$），表示第一个灯笼的位置； - 第三行包含两个整数 $B_x$ 和 $B_y$（$-10^3 \le B_x, B_y \le 10^3$），表示第二个灯笼的位置。 输入的额外约束： - 每个测试用例中，点 $O$、$P$、$A$ 和 $B$ 互不相同。

对于每个测试用例，输出一行，一个实数，表示最小的亮度 $w$，使得存在一条从点 $O$ 到点 $P$ 的路径，且这条路径完全被照亮。 如果你的答案的绝对误差或相对误差不超过 $10^{-6}$，则视为正确。形式化地说，如果你的答案为 $a$，标准答案为 $b$，则当 $\dfrac{|a - b|}{\max(1, b)} \le 10^{-6}$ 时，你的答案会被接受。

由 ChatGPT 4.1 翻译