CF1889E Doremy's Swapping Trees

给定两个无向图 $G_1$ 和 $G_2$，每个图中的每个节点都有一个标签。Doremy 认为 $G_1$ 和 $G_2$ 是相似的，当且仅当： - $G_1$ 和 $G_2$ 中的标签各不相同。 - $G_1$ 的标签集合 $S$ 与 $G_2$ 的标签集合相同。 - 对于 $S$ 中任意两个不同的标签 $u$ 和 $v$，如果它们在 $G_1$ 中属于同一个连通分量，当且仅当它们在 $G_2$ 中也属于同一个连通分量。 现在，Doremy 给你两棵有 $n$ 个节点的树 $T_1$ 和 $T_2$，节点编号为 $1$ 到 $n$。你可以进行如下操作任意次： - 从 $T_1$ 中选择一个边集 $E_1$，从 $T_2$ 中选择一个边集 $E_2$，使得 $\overline{E_1}$ 和 $\overline{E_2}$ 是相似的。这里 $\overline{E}$ 表示仅保留边集 $E$ 的图（即边诱导子图）。换句话说，$\overline{E}$ 是从 $T$ 中移除所有不在 $E$ 中的边，并进一步移除所有孤立点后得到的图。 - 将 $T_1$ 中的边集 $E_1$ 与 $T_2$ 中的边集 $E_2$ 交换。 现在 Doremy 想知道，经过任意次数的操作后，$T_1$ 最多能得到多少种不同的形态。请你帮她计算答案，并对 $10^9+7$ 取模。

输入包含多组测试数据。第一行包含一个整数 $t$（$1\le t\le 2\times 10^4$），表示测试用例的数量。 每组测试数据的第一行包含一个整数 $n$（$2\le n\le 10^5$），表示树 $T_1$ 和 $T_2$ 的节点数。 接下来的 $n-1$ 行，每行包含两个整数 $u,v$（$1\le u,v\le n$），表示 $T_1$ 中的一条无向边。保证这些边构成一棵树。 接下来的 $n-1$ 行，每行包含两个整数 $u,v$（$1\le u,v\le n$），表示 $T_2$ 中的一条无向边。保证这些边构成一棵树。 保证所有测试用例中 $n$ 的总和不超过 $2\times 10^5$。

对于每个测试用例，输出一行一个整数，表示经过任意次数操作后，$T_1$ 最多能得到多少种不同的形态，对 $10^9+7$ 取模。

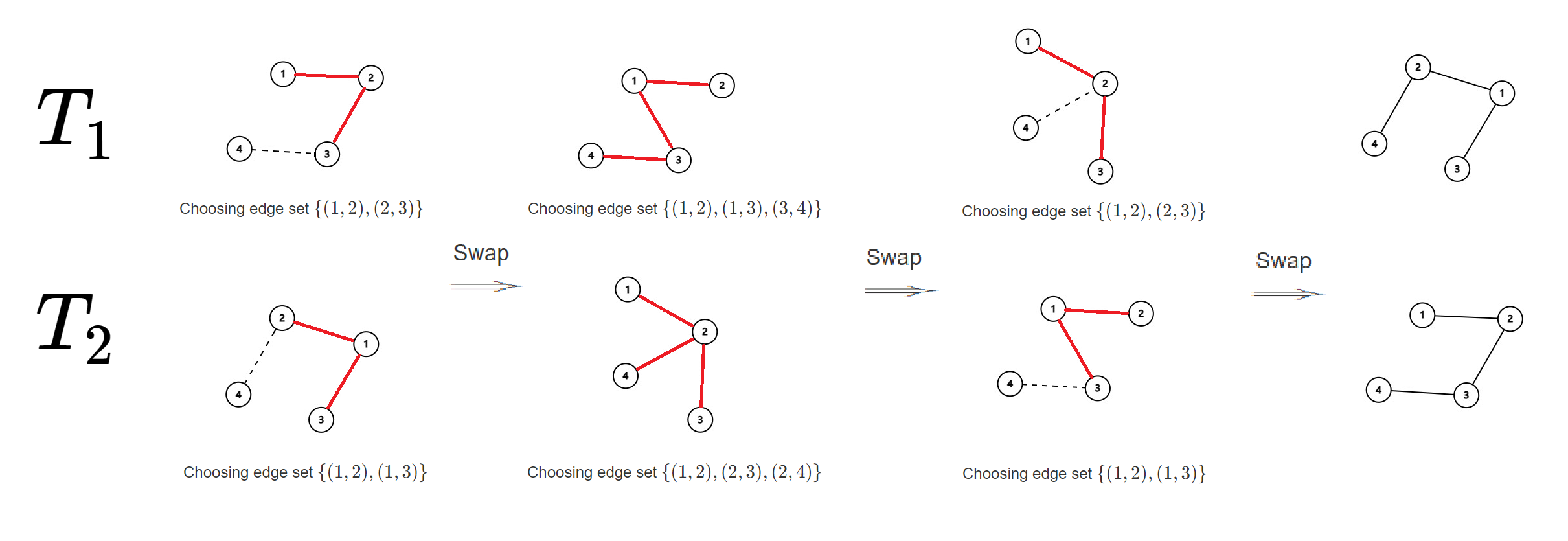
在第一个测试用例中，最多只有一种不同的 $T_1$，即只包含边 $(1,2)$。 在第二个测试用例中，你可以选择 $T_1$ 中的边集 $\{(1,3),(2,3)\}$，$T_2$ 中的边集 $\{(1,2),(2,3)\}$ 并交换它们。因此 $T_1$ 可以是 $1-3-2$ 或 $1-2-3$。 在第三个测试用例中，有 $4$ 种不同的 $T_1$，如下图所示。  由 ChatGPT 4.1 翻译