CF1889F Doremy's Average Tree

你有一棵大小为 $n$，根节点为 $r$ 的树，节点 $i$ 的权值是 $w_i$。你可以执行以下操作**至多** $k$ 次： 选择一个节点 $x$，令 $s$ 为 $x$ 子树内所有点权值的平均值，把 $x$ 子树内所有点的权值修改为 $s$。 你现在想让操作后的 $w$ 数组的字典序最小，请构造一种满足条件的方案。

有多组测试数据。第一行一个整数 $t(1\leq t\leq 10^4)$，表示测试数据的组数。 每组数据第一行三个整数 $n,r,k(2\leq n\leq 5000,1\leq r \leq n,0\leq k\leq\min(500,n))$。 第二行有 $n$ 个正整数，第 $i$ 个表示点 $i$ 的初始权值，保证其不超过 $10^6$。 接下来 $n-1$ 行每行两个数 $u_i,v_i(1\leq u_i,v_i\leq n)$，表示有一条连接 $u_i,v_i$ 的边。 保证所有数据中 $n$ 的总和不超过 $5\times 10^4$，输入的是一棵树。

每组数据两行，第一行表示你操作的次数 $k$，第二行 $k$ 个数，表示每次操作中你选择的 $x$。 如果有多种答案，你可以输出任意一种。

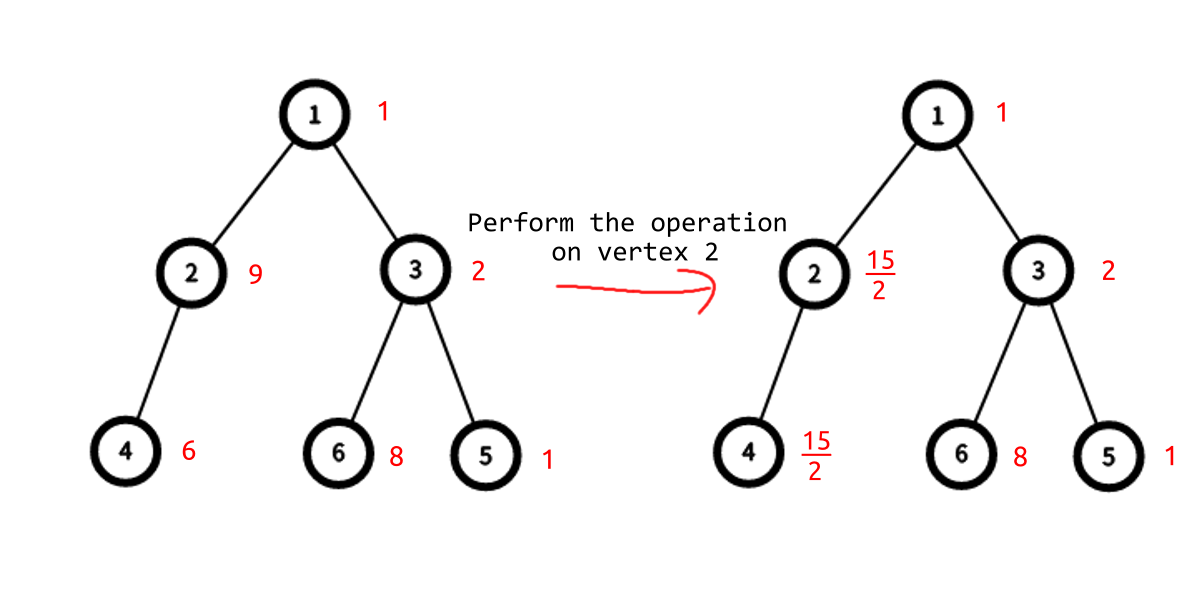
In the first test case:  At first $ w=[1,9,2,6,1,8] $ . You can choose some vertex $ x $ to perform at most one operation. - If $ x=1 $ , $ w=[\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2}] $ . - If $ x=2 $ , $ w=[1,\frac{15}{2},2,\frac{15}{2},1,8] $ . - If $ x=3 $ , $ w=[1,9,\frac{11}{3},6,\frac{11}{3},\frac{11}{3}] $ . - If $ x \in \{4, 5, 6\} $ , $ w=[1,9,2,6,1,8] $ . - If you don't perform any operation, $ w=[1,9,2,6,1,8] $ . $ w $ is lexicographically smallest when $ x=2 $ .