CF1889F Doremy's Average Tree

Doremy has a rooted tree of size $ n $ whose root is vertex $ r $ . Initially there is a number $ w_i $ written on vertex $ i $ . Doremy can use her power to perform this operation at most $ k $ times: 1. Choose a vertex $ x $ ( $ 1 \leq x \leq n $ ). 2. Let $ s = \frac{1}{|T|}\sum_{i \in T} w_i $ where $ T $ is the set of all vertices in $ x $ 's subtree. 3. For all $ i \in T $ , assign $ w_i := s $ . Doremy wants to know what is the lexicographically smallest $ ^\dagger $ array $ w $ after performing all the operations. Can you help her? If there are multiple answers, you may output any one. $ ^\dagger $ For arrays $ a $ and $ b $ both of length $ n $ , $ a $ is lexicographically smaller than $ b $ if and only if there exist an index $ i $ ( $ 1 \leq i \le n $ ) such that $ a_i < b_i $ and for all indices $ j $ such that $ j

The input consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1\le t\le 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line contains three integers $ n $ , $ r $ , $ k $ ( $ 2 \le n \le 5000 $ , $ 1 \le r \le n $ , $ 0 \le k \le \min(500,n) $ ). The second line contains $ n $ integers $ w_1,w_2,\ldots,w_n $ ( $ 1 \le w_i \le 10^6 $ ). Each of the next $ n-1 $ lines contains two integers $ u_i $ , $ v_i $ ( $ 1 \leq u_i, v_i \leq n $ ), representing an edge between $ u_i $ and $ v_i $ . It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ does not exceed $ 50\,000 $ .

For each test case, In the first line, output a single integer $ cnt $ ( $ 0 \le cnt \le k $ ) — the number of operations you perform. Then, in the second line output $ cnt $ integers $ p_1,p_2,\ldots,p_{cnt} $ — $ x $ is chosen to be $ p_i $ for $ i $ -th operation. If there are multiple answers, you may output any one.

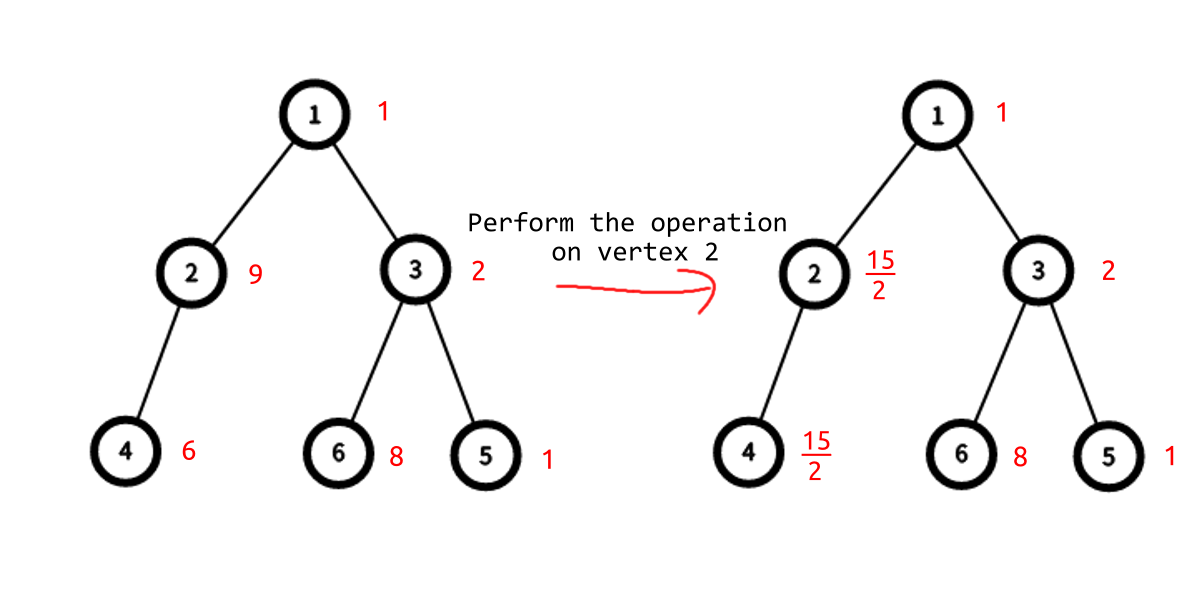
In the first test case:  At first $ w=[1,9,2,6,1,8] $ . You can choose some vertex $ x $ to perform at most one operation. - If $ x=1 $ , $ w=[\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2}] $ . - If $ x=2 $ , $ w=[1,\frac{15}{2},2,\frac{15}{2},1,8] $ . - If $ x=3 $ , $ w=[1,9,\frac{11}{3},6,\frac{11}{3},\frac{11}{3}] $ . - If $ x \in \{4, 5, 6\} $ , $ w=[1,9,2,6,1,8] $ . - If you don't perform any operation, $ w=[1,9,2,6,1,8] $ . $ w $ is lexicographically smallest when $ x=2 $ .