CF1891F A Growing Tree

You are given a rooted tree with the root at vertex $ 1 $ , initially consisting of a single vertex. Each vertex has a numerical value, initially set to $ 0 $ . There are also $ q $ queries of two types: - The first type: add a child vertex with the number $ sz + 1 $ to vertex $ v $ , where $ sz $ is the current size of the tree. The numerical value of the new vertex will be $ 0 $ . - The second type: add $ x $ to the numerical values of all vertices in the subtree of vertex $ v $ . After all queries, output the numerical value of all of the vertices in the final tree.

The first line contains a single integer $ T $ ( $ 1 \leq T \leq 10^4 $ ) — the number of test cases. The descriptions of the test cases follow. The first line of each test case contains a single integer $ q $ ( $ 1 \leq q \leq 5 \cdot 10^5 $ ) — the number of queries. The following $ q $ lines can fall into two cases: - The first type of query: The $ i $ -th line contains two integers $ t_i $ ( $ t_i = 1 $ ), $ v_i $ . You need to add a child with the number $ sz + 1 $ to vertex $ v_i $ , where $ sz $ is the current size of the tree. It is guaranteed that $ 1 \leq v_i \leq sz $ . - The second type of query: The $ i $ -th line contains three integers $ t_i $ ( $ t_i = 2 $ ), $ v_i $ , $ x_i $ ( $ -10^9 \leq x_i \leq 10^9 $ ). You need to add $ x_i $ to all numerical values of vertices in the subtree of $ v_i $ . It is guaranteed that $ 1 \leq v_i \leq sz $ , where $ sz $ is the current size of the tree. It is guaranteed that the sum of $ q $ across all test cases does not exceed $ 5 \cdot 10^5 $ .

For each test case, output the numerical value of each vertex of the final tree after all queries have been performed.

In the first case, the final tree with the assigned numerical values will look like this: 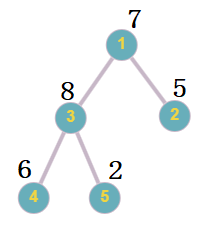 The final tree with the assigned numerical values