CF1898C Colorful Grid

Elena 有一个由 $n$ 条水平线和 $m$ 条垂直线组成的网格。水平线从上到下编号为 $1$ 到 $n$，垂直线从左到右编号为 $1$ 到 $m$。对于每个 $x$ 和 $y$（$1 \leq x \leq n$，$1 \leq y \leq m$），记号 $(x, y)$ 表示第 $x$ 条水平线与第 $y$ 条垂直线的交点。 两个点 $(x_1, y_1)$ 和 $(x_2, y_2)$ 当且仅当 $|x_1-x_2| + |y_1-y_2| = 1$ 时相邻。  上图为 $n=4$ 条水平线和 $m=5$ 条垂直线组成的网格。 Elena 称长度为 $g$ 的点序列 $p_1, p_2, \ldots, p_g$ 为一次“行走”，当且仅当满足以下所有条件： - 序列的第一个点 $p_1$ 是 $(1, 1)$。 - 序列的最后一个点 $p_g$ 是 $(n, m)$。 - 对于每个 $1 \leq i < g$，点 $p_i$ 和 $p_{i+1}$ 是相邻的。 注意，行走过程中可以多次经过同一个点，特别是 $(1, 1)$ 或 $(n, m)$ 可以出现多次。 在 Elena 的网格中，相邻点之间一共存在 $n(m-1)+(n-1)m$ 条线段。Elena 想要将这些线段分别涂成蓝色或红色，使得存在一条长度为 $k+1$ 的行走 $p_1, p_2, \ldots, p_{k+1}$，满足： - 在该行走中，连接连续两点的 $k$ 条线段中，任意相邻的两条线段颜色不同（即对于每个 $1 \leq i < k$，点 $p_i$ 与 $p_{i+1}$ 之间的线段颜色与 $p_{i+1}$ 与 $p_{i+2}$ 之间的线段颜色不同）。 请你找出一种满足条件的涂色方案，或者报告不存在这样的方案。

每组测试包含多组数据。第一行包含一个整数 $t$（$1 \leq t \leq 32$），表示测试用例的数量。 每组测试的唯一一行包含三个整数 $n$、$m$ 和 $k$（$3 \leq n, m \leq 16$，$1 \leq k \leq 10^9$），分别表示网格的行数、列数，以及 Elena 期望的行走所经过的线段数。

对于每组测试数据，如果不存在满足条件的涂色方案，输出一行 "NO"。 否则，第一行输出 "YES"，然后输出所需的涂色方案。 在接下来的 $n$ 行中，每行输出 $m-1$ 个用空格分隔的字符，第 $i$ 行第 $j$ 个字符表示点 $(i, j)$ 与 $(i, j+1)$ 之间线段的颜色。用 'B' 表示蓝色，'R' 表示红色。 在接下来的 $n-1$ 行中，每行输出 $m$ 个用空格分隔的字符，第 $i$ 行第 $j$ 个字符表示点 $(i, j)$ 与 $(i+1, j)$ 之间线段的颜色。同样用 'B' 表示蓝色，'R' 表示红色。 答案中字母大小写均可。例如，"yEs"、"yes"、"Yes" 和 "YES" 都被视为肯定回答，'R' 和 'r' 都表示红色。

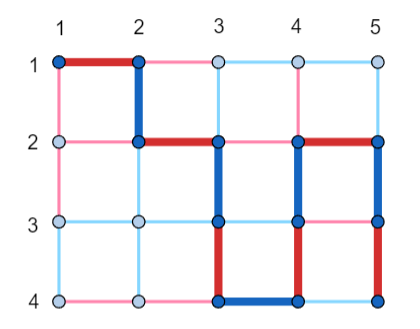
在第一个测试用例中，下面的图片展示了一个正确答案。长度为 $12$ 的颜色交替行走已被高亮显示。  在第二个和第三个测试用例中，可以证明不存在满足条件的涂色方案。 由 ChatGPT 4.1 翻译